 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVII олимпиада, 1996-1997 >> Областной тур >> 8 класс >> 1-й день | Убрать решения |
|
|
| XXXVII Екатеринбургская городская олимпиада, 1996-1997. Областной тур. 8 класс. 1-й день |
|
|
Известно, что одно из натуральных чисел x и y чётно, а другое – нечётно. Представить число xy + x в виде разности квадратов двух целых чисел.
(Рекомендована жюри Российской олимпиады.)
Решение: Число xy + x = x(y + 1) либо нечётно, либо делится на 4. В первом случае искомым представлением будет ,
во втором –
,
во втором – 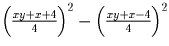 .
Задача 2:
.
Задача 2: Назовём натуральные числа близкими, если их десятичная запись содержит одно и то же число значащих цифр и отличается ровно в одном разряде на величину, по модулю равную 1.
Докажите, что если трёхзначное число не начинается с 1 и не содержит в своей записи нулей и девяток, то либо оно само, либо одно из близких ему чисел делится на 7.
((Предложена С.Э.Нохриным.))
Решение: Отсутствие 0 и 9 в записи числа a дает нам возможность утверждать, что близкими к a будут числа a – 1,a + 1, a – 10, a + 10, a – 100, a + 100. Очевидно, что все эти числа, а также число a, имеют разные остатки от деления на 7. Поскольку среди остатков есть 0, то задача решена. Задача 3:На окружности отмечено 1997 точек. Рассматриваются всевозможные выпуклые многоугольники с вершинами в этих точках. Пусть A – одна из отмеченных точек. Каких многоугольников больше – содержащих вершину A или не содержащих её?
((Предложена Е.С.Зенковой.))
Решение: Каждому n-угольнику, не содержащему вершину A, соответствует однозначно определенный n + 1-угольник, её содержащий. Вершинами этого n + 1-угольника являются вершины n-угольника и сама вершина A. При этом все содержащие A треугольники оказываются незадействованными. Отсюда многоугольников, содержащих A, больше. Задача 4:Прямоугольник вписан в квадрат таким образом, что его стороны не параллельны диагоналям квадрата. Докажите, что этот прямоугольник также является квадратом. (Считаем, что прямоугольник вписан в квадрат, если на каждой стороне квадрата лежит вершина прямоугольника.)
((Предложена В.В.Кабановым.))
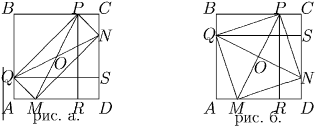
Решение:первый способ. Пусть ABCD – квадрат, MNPQ – вписанный в него прямоугольник, причем M ∈ AD, N ∈ CD, P ∈ BC, Q ∈ AB (см. рис.a, б). Проведём в MNPQ диагонали и опустим из точек P и Q на стороны квадрата перпендикуляры с основаниями R и S, соответственно. Треугольники ∆ PMR и ∆ QNS равны, так как имеют равные гипотенузы и равные катеты PR и QS. Тогда MR = SN. Пусть AM = x, MD = y, CN = u, ND = v. Очевидно, что MR = |y – x|, SN = |u – v|. С другой стороны, x + y = AD = CD = u + v. Из условия, что стороны прямоугольника не параллельны диагоналям квадрата, следует, что x ≠ u, y ≠ v (случай, изображённый на рис.а, невозможен). Но тогда x = v, y = u. Значит, треугольники ∆ QMA и ∆ MND равны, и MNPQ – квадрат.
второй способ.
Из подобия треугольников MAQ и MDN имеем:  ,
но x + y = v + u, откуда
,
но x + y = v + u, откуда  , (u + v)(y – u) = 0, и y = u,
а значит x = v, ∆ QMA = ∆ MND,
и MNPQ – квадрат.
, (u + v)(y – u) = 0, и y = u,
а значит x = v, ∆ QMA = ∆ MND,
и MNPQ – квадрат.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVII олимпиада, 1996-1997 >> Областной тур >> 8 класс >> 1-й день | Убрать решения |