Задача 1:
Докажите, что
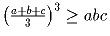
,
при всех неотрицательных a, b, и c.
Решение:
Пусть c – наибольшее из данных трёх чисел, и пусть
c = m + d, где
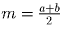
. Тогда d неотрицательно,
а левая часть неравенства записывается в виде
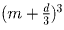
.
Легко видеть, что это выражение не меньше, чем m³ + m²d = m²c.
Остаётся доказать, что m² ≥ ab, что немедленно следует из
равенства
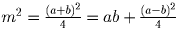
.
Задача 2:
Даны простые числа p и q, причём q³ – 1 делится на p, и
p – 1 делится на q. Докажите, что p = 1 + q + q².
Решение:
q³ – 1 = (q – 1)(q² + q + 1) делится на p. Учитывая, что p –
простое,и p > q (так как p – 1 делится на q), имеем
q² + q + 1 = α p, где α – натуральное число. Ясно также,
что для некоторого натурального β справедливо p – 1 = β q.
Сложив почленно оба уравнения, получим: q(q + 1 – β ) = p( α – 1).
Так как ни q, ни q + 1 – β на p не делятся (оба эти числа
меньше p), имеем α – 1 = 0, откуда q² + q + 1 = p, ч.т.д.
Задача 3:
Как сварить яйца за 15 минут, пользуясь песочными
часами на 7 и 11 минут?
Решение:
Так как 15 = 2 • 11 – 7, достаточно запустить одновременно те и
другие часы, начать отваривать яйца, когда впервые высыпется песок из
семиминутных часов, а завершить – когда песок во второй раз
высыпется из одиннадцатиминутных.
Задача 4:
Точки A
1, B
1 и C
1 взяты соответственно на
сторонах AB, BC и AC треугольника ABC так, что
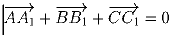
. Докажите, что
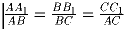
.
Решение:
Пусть
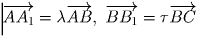
, и
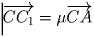
. Из условия
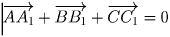
, учитывая, что
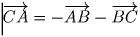
,
получаем:
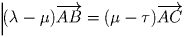
. Так как векторы
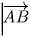
и
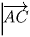
не коллинеарны, λ – μ = μ – τ = 0,
откуда λ = μ = τ . Остаётся заметить, что
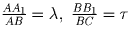
, и
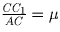
.


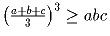 ,
при всех неотрицательных a, b, и c.
Решение:
Пусть c – наибольшее из данных трёх чисел, и пусть
c = m + d, где
,
при всех неотрицательных a, b, и c.
Решение:
Пусть c – наибольшее из данных трёх чисел, и пусть
c = m + d, где 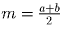 . Тогда d неотрицательно,
а левая часть неравенства записывается в виде
. Тогда d неотрицательно,
а левая часть неравенства записывается в виде
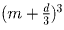 .
Легко видеть, что это выражение не меньше, чем m³ + m²d = m²c.
Остаётся доказать, что m² ≥ ab, что немедленно следует из
равенства
.
Легко видеть, что это выражение не меньше, чем m³ + m²d = m²c.
Остаётся доказать, что m² ≥ ab, что немедленно следует из
равенства 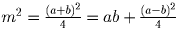 .
.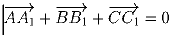 . Докажите, что
. Докажите, что
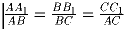 .
Решение:
Пусть
.
Решение:
Пусть 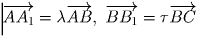 , и
, и 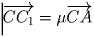 . Из условия
. Из условия
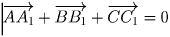 , учитывая, что
, учитывая, что
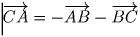 ,
получаем:
,
получаем: 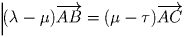 . Так как векторы
. Так как векторы 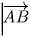 и
и
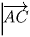 не коллинеарны, λ – μ = μ – τ = 0,
откуда λ = μ = τ . Остаётся заметить, что
не коллинеарны, λ – μ = μ – τ = 0,
откуда λ = μ = τ . Остаётся заметить, что
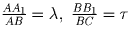 , и
, и
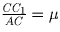 .
.