Задача 1:
Докажите, что для любых неотрицательных чисел a, b и c
справедливо неравенство:
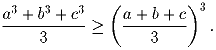
Решение:
Пусть a + b + c = 3m, a = m + a
1, b = m + b
1, c = m + c
1. Ясно, что
a
1 + b
1 + c
1 = 0. Легко видеть, что a³ = (a
1 + m)³ ≥ m³ + 3a
1m². Аналогично, b³ ≥ m³ + 3b
1m² и
c³ ≥ m³ + 3c
1m². Сложив почленно все три неравенства,
умноженные каждое на ⅓, и заменив m на
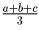
, получим требуемое.
Задача 2:
Покажите, что уравнение x³ + x = y²
не имеет целочисленных решений кроме x = y = 0.
Решение:
Числа x и x² + 1 взаимно-просты (то есть не имеют общих
делителей, отличных от ± 1 поэтому из условия
y² = x³ + x = x(x² + 1) следует, что как x, так и x² + 1
является точным квадратом. Но x² + 1 является точным квадратом
только при x = 0 (докажите!), что завершает доказательство.
Задача 3:
На окружности даны 20 точек. Двое по очереди проводят хорды с
концами в этих точках так, чтобы хорды не пересекались. Проигрывает тот,
кто не сможет провести хорду. Кто победит при правильной игре –
начинающий, или его партнёр?
Решение:
Занумеруем точки натуральными числами от 1 до 20 в порядке их
следования по часовой стрелке (начинать можно с произвольной точки).
Одна из стратегий начинающего, гарантирующая ему выигрыш, такова:
первым ходом он соединяет точки 10 и 20. Теперь хорды, соединяющие
точку с номером меньше 10 с точкой, номер которой больше 10,
«запрещены". Далее начинающий играет симметрично своему оппоненту,
то есть на хорду, соединяющую точки i и j, при i, j < 10 он
отвечает хордой через точки с номерами i + 10 и j + 10 и наоборот.
Очевидно, у него при такой стратегии всегда будет возможность сделать
свой ход.
Задача 4:
Используя неравенство
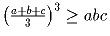
,
справедливое для любых положительных чисел a, b и c, докажите,
что из всех треугольников с данным периметром наибольшую площадь
имеет правильный треугольник.
Решение:
Пусть 2p = a + b + c – заданный периметр, а S – площадь
треугольника со сторонами a, b и c. По формуле Герона
S² = p(p – a)(p – b)(p – c). Cогласно неравенству, приведённому в
условии,
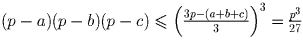
, поэтому
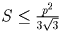
. Остаётся заметить, что в
последнем неравенстве справа стоит площадь правильного треугольника
периметра 2p.


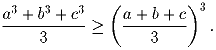
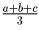 , получим требуемое.
Задача 2:
Покажите, что уравнение x³ + x = y²
не имеет целочисленных решений кроме x = y = 0.
, получим требуемое.
Задача 2:
Покажите, что уравнение x³ + x = y²
не имеет целочисленных решений кроме x = y = 0.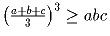 ,
справедливое для любых положительных чисел a, b и c, докажите,
что из всех треугольников с данным периметром наибольшую площадь
имеет правильный треугольник.
Решение:
Пусть 2p = a + b + c – заданный периметр, а S – площадь
треугольника со сторонами a, b и c. По формуле Герона
S² = p(p – a)(p – b)(p – c). Cогласно неравенству, приведённому в
условии,
,
справедливое для любых положительных чисел a, b и c, докажите,
что из всех треугольников с данным периметром наибольшую площадь
имеет правильный треугольник.
Решение:
Пусть 2p = a + b + c – заданный периметр, а S – площадь
треугольника со сторонами a, b и c. По формуле Герона
S² = p(p – a)(p – b)(p – c). Cогласно неравенству, приведённому в
условии, 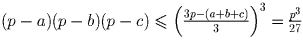 , поэтому
, поэтому
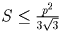 . Остаётся заметить, что в
последнем неравенстве справа стоит площадь правильного треугольника
периметра 2p.
. Остаётся заметить, что в
последнем неравенстве справа стоит площадь правильного треугольника
периметра 2p.