Задача 1:
Доказать, что
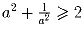
, где a –
некоторое число.
Решение:
Так как
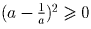
, то
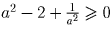
,
откуда
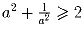
, что и требовалось доказать.
Задача 2:
Пусть M – натуральное число.
Доказать, что число M(M + 1)(M + 2)(M + 3) делится на 24.
Решение:
Так как среди любых четырех последовательных натуральных чисел
имеется два
четных, причём одно из них делится на 4, произведение
M(M + 1)(M + 2)(M + 3) делится на 8. Кроме того, среди чисел
M, (M + 1), (M + 2), (M + 3) найдется число, которое делится на 3.
Следовательно, произведение M(M + 1)(M + 2)(M + 3) делится на 24,
что и требовалось доказать.
Задача 3:
Сколькими способами четыре разные книги можно поставить на
книжную полку?
Решение:
На первом месте может находиться любая из четырех книг, на
втором – любая из трех оставшихся, на третьем – любая из двух
оставшихся. Таким образом, всего способов 4 • 3 • 2 • 1 = 24.


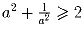 , где a –
некоторое число.
, где a –
некоторое число.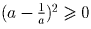 , то
, то 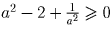 ,
откуда
,
откуда 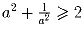 , что и требовалось доказать.
, что и требовалось доказать.