 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVII олимпиада, 1996-1997 >> Районный тур >> 8 класс | Убрать решения |
|
|
| XXXVII Екатеринбургская городская олимпиада, 1996-1997. Районный тур. 8 класс |
|
|
Решение: Искомое разложение: x4 + 4y4 = (x² + 2y²)² – (2xy)² = (x² + 2y² – 2xy)(x² + 2y² + 2xy).
Задача 2: Доказать, что если между цифрами числа 1331 вставить по равному количеству нулей, то получится точный куб.
Решение: Пусть между цифрами данного числа вставлено по n нулей. Тогда образуется число 1 • 103n + 3 • 102n + 3 • 10n + 1, равное (1 + 10n)³.
Задача 3: Группа из 21 мальчика собрала 200 орехов. Докажите, что двое из них собрали одинаковое количество орехов.
Решение: Пусть все мальчики собрали разное число орехов, и пусть i-ый собрал ai штук. Без ограничения общности a1 < a2 < … < a21. Так как все ai – целые неотрицательные числа, имеем a1 ≥ 0, a2 ≥ 1, …, a21 ≥ 20. Но тогда a1 + a2 + … + a21 ≥ 210 > 200 – противоречие.
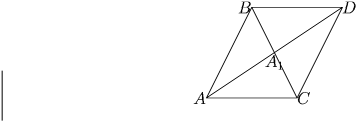
Задача 4: Докажите, что медиана треугольника меньше полусуммы сторон ее заключающих и больше разности между этой полусуммой и половиной третьей стороны.
Решение: Достроим треугольник до параллелограмма ABDC (см. рисунок). Тогда его медиана AA1 будет равна половине диагонали AD. В треугольнике ADC сторона AD меньше суммы двух других сторон AC и CD. Отсюда вытекает первое утверждение. Рассмотрим далее два треугольника AA1C, A1DC. В первом из них сторона AA1 больше разности сторон AC – A1C. Во втором – сторона A1D больше разности сторон DC – A1C. Если просуммировать эти два неравенства и разделить то что получится на два, то получится второе утверждение.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVII олимпиада, 1996-1997 >> Районный тур >> 8 класс | Убрать решения |