Задача 1: Три гонщика (A, потом B и затем C) стартуют с интервалом 1 мин. из одной точки кольцевого шоссе и двигаются в одном направлении с постоянными скоростями. Каждый гонщик затрачивает на круг более двух минут. Сделав три круга, гонщик A в первый раз догоняет B у точки старта, а еще через три минуты он вторично обгоняет C. Гонщик B впервые догнал C также у точки старта, закончив 4 круга. Сколько минут тратит на круг гонщик A?

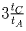Решение: Пусть t_A, t_B и t_C – время в минутах, затрачиваемое на 1 круг гонщиками A, B и C соответственно. Тогда на 3 круга гонщик A затрачивает 3t_A минут, что на 1 минуту больше, чем требуется гонщику B на 2 круга, поэтому 3t_A – 1 = 2t_B  (1). Аналогично получаем 4t_B – 1 = 3t_C  (2). На прохождение расстояния, которое гонщик A пройдет в 3 минуты, гонщику C потребуется минут, поэтому время, которое гонщик C был в пути до того, как A его вторично обогнал равно . Имеем: 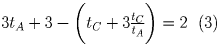. Решая систему уравнений (1) – (3), и учитывая, что t_A > 2, находим: t_A = 3.

Задача 2:

Над планетой, имеющей форму шара, летают три спутника. Докажите, что в любой момент времени на поверхности планеты имеется точка, из которой ни один из спутников не виден. Спутники считаются точечными.

Проведём плоскость через 3 точки – спутника, и восстановим к ней перпендикуляр из центра планеты. Пусть он пересекает поверхность планеты в точках A и B, а проведённую плоскость в точке C. Тогда если AC ≥ BC, то из точки A не видна вся проведённая плоскость, а поэтому и все спутники. Если же AC < BC, то таким свойством обладает точка B.

Задача 3: Докажите, что уравнение m! • n! = k! имеет бесконечно много решений таких, что n, m и k – натуральные числа, большие 1.

Решение: Для любого натурального числа a > 2 тройка n = a, m = a! – 1, k = a! является решением.

Задача 4:

Изобразите на плоскости AOB множество пар (a;b), таких что ситема уравнений

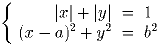
а) имеет ровно 8 решений;

б) имеет ровно 7 решений;

в) не имеет решений;

Решение: На плоскости XOY множество точек, удовлетворяющих первому уравнению системы, – есть граница квадрата с диагоналями, лежащими на осях координат, а второе уравнение задаёт окружность радиуса |b| с центром в точке (a;0). Ввиду очевидной симметрии в дальнейшем мы будем рассматривать только случай a, b ≥ 0.

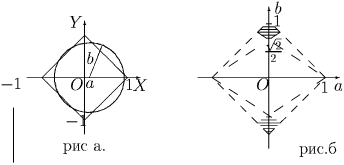
а) Окружность и граница квадрата имеют восемь общих точек тогда и только тогда, когда расстояние от центра окружности до каждого из углов квадрата больше радиуса, а до любой стороны – меньше радиуса (см. рис.5а.). Это выполняется при условии: 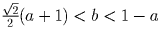. Искомое множество приведено на рис. 5б.

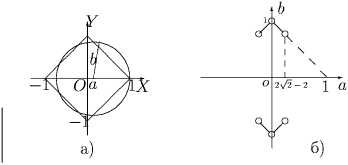
б) Так как число решений нечётно, ровно одна из точек пересечения лежит на оси OX, и это может быть (при a > 0) только точка (1;0). Имеем: b = 1 – a. Кроме того, расстояние от центра окружности до каждой из сторон квадрата не превосходит радиуса, откуда 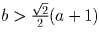(см. рис. а). Ещё заметим, что при a = 0 решений нет, так как в этом случае точки ( – 1;0) и (1;0) удовлетворяют или не удовлетворяют системе одновременно. Ответ приведён на рис. б.

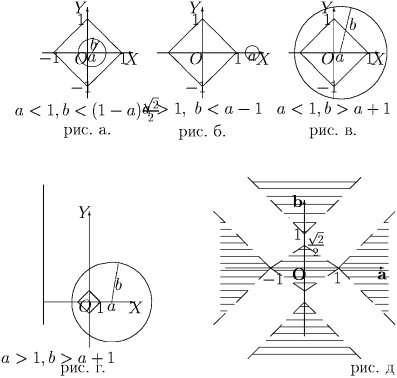
в) Система не будет иметь решений в случаях, изображённых на рисунках а-г. Соответствующие ограничения написаны под рисунками, а искомое множество изображено на рис д.