 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVII олимпиада, 1996-1997 >> Заочный тур >> 11 класс | Убрать решения |
|
|
| XXXVII Екатеринбургская городская олимпиада, 1996-1997. Заочный тур. 11 класс |
|
|
б) Другой кузнечик делает первый прыжок на (½)² дм, второй – на (⅓)² дм, и т.д. Сможет ли он пропрыгать те же 10 дм?
Решение: Рассмотрим расстояние, которое пропрыгает кузнечик за N шагов, то есть подсчитаем сумму
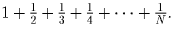 Для этого отбросив 1, разобьем ее
на группы
Для этого отбросив 1, разобьем ее
на группы 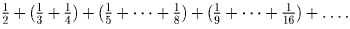 Каждая
группа содержит 2k + 1 – 2k = 2k членов, каждый из которых не меньше
чем последний член, равный
Каждая
группа содержит 2k + 1 – 2k = 2k членов, каждый из которых не меньше
чем последний член, равный 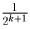 ; величина группы
поэтому больше, чем
; величина группы
поэтому больше, чем 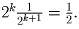 Таким
образом, если мы возьмем достаточное число групп, то получим
расстояние большее 11.
Таким
образом, если мы возьмем достаточное число групп, то получим
расстояние большее 11.
Рассмотрим теперь сумму
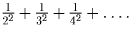 Разобьем ее на
группы
Разобьем ее на
группы 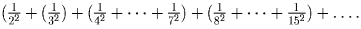 Каждая группа Каждая группа содержит 2k + 1 – 2 – 2k + 1 + 1 = 2k членов,
каждый из которых не больше первого члена, равного
Каждая группа Каждая группа содержит 2k + 1 – 2 – 2k + 1 + 1 = 2k членов,
каждый из которых не больше первого члена, равного 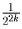 ; величина группы поэтому не больше, чем
; величина группы поэтому не больше, чем
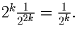 Таким образом, Но тогда сумма
всех групп не больше чем сумма членов бесконечной убывающей
геометрической прогрессии. Подсчитав эту сумму убеждаемся, что
кузнечик не сможет покрыть данное расстояние.
Таким образом, Но тогда сумма
всех групп не больше чем сумма членов бесконечной убывающей
геометрической прогрессии. Подсчитав эту сумму убеждаемся, что
кузнечик не сможет покрыть данное расстояние.
Задача 2:
Решите в целых числах уравнение 2y + 7 = x².
Решение: Заметим, что y ≥ 0 (иначе 2y – не целое число, а x² – целое число. Противоречие.)
Пусть y = 0. Тогда x² = 2º + 7 = 7. Но 7 не является квадратом.
Пусть y = 1. Тогда x² = 2¹ + 7 = 9. Отсюда y = ± 3.
Пусть y > 1. Тогда 2y является четным числом. В то же время x² = 2y + 7 является нечетным числом. Значит, и x является нечетным числом. Пусть x = 2n + 1. Тогда x² = 4n² + 4n + 1. Отсюда 2y + 6 = 4(n² + n). Поскольку y ≥ 2, то 2y делится на 4. Поскольку левая часть уравнения делится на 4, то 6 также делится на 4. Противоречие.
Задача 3: На плоскости лежат три шара одинакового диаметра d, которые касаются друг друга и вписаны в конус высоты h, с основанием в той же плоскости. Найти длину образующей конуса. Решение: Выберем один из данных шаров. Проведем плоскость через ось конуса BC и центр шара O. Рассмотрим сечение конуса (см. рис.8.). Пусть AB – образующая конуса и l = AB, h = BC, r – радиус шара, x = AM, y = BM, где M – точка касания шара и конуса в плоскости сечения. Кроме того пусть z = OB – длина отрезка, соединяющего центр шара и вершину конуса, w = NC, где N – точка касания шара и плоскости основания конуса. Заметим, что AN = AM = x.
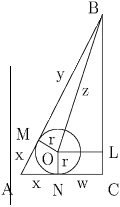
1. По теореме Пифагора для ∆ ABC имеем
l² = h² + (x + w)². Кроме того l = x + y, поэтому
x² + 2xy + y² = h² + x² + 2xw + w².
Отсюда 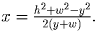
2. Поскольку шары касаются друг друга, то их центры образуют
правильный треугольник. Следовательно, 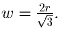
3. По теореме Пифагора для ∆ OBL имеем
z² = (h – r)² + w². Аналогично, из ∆ MOB
y² = z² – r². То есть 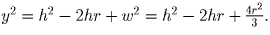
4. Подставим найденное значение y в найденное выражение для x.
Получаем равенство:
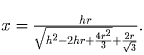
5. Итак, поскольку l = x + y, то
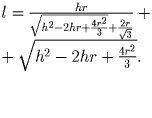
Задача 4:
Лист клетчатой бумаги размера 10 × n заполнен карточками так, что каждая карточка занимает в точности две соседние клетки. На каждой карточке написаны два числа + 1 и – 1 таким образом, что на листе получается 10 × n таблица. Найдите все возможные n при которых произведение чисел в каждом столбце таблицы положительно.
Решение: Произведение чисел в каждом столбце таблицы положительно по условию задачи, значит, произведение всех чисел в таблице также положительно. В таблице будет 5n клеток содержащих 1 и 5n клеток содержащих – 1. Таким образом произведение всех чисел в таблице будет отрицательным при нечетном n и положительным при четном n. То есть четность числа n является необходимым условием. Легко видеть, что найденное условие является достаточным.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVII олимпиада, 1996-1997 >> Заочный тур >> 11 класс | Убрать решения |