Задача 1:
Решить уравнение: |3x – 14| = |2x – 1|.
Решение:
Для x > 4⅔ имеем 3x – 14 = 2x – 1, откуда x = 13.
Для ½ < x < 4⅔ имеем – 3x + 14 = 2x – 1, откуда x = 3.
Для ½ > x решений нет.
Задача 2:
Докажите, что разность 43
43 – 17
77 делится на 10
без остатка.
Решение:
Достаточно доказать, что 43
43 и 17
77 оканчиваются на
одно и то же число. Заметим, что 3
4k оканчивается на 1,
3
4k + 1 – на 3, 3
4k + 2 – на 9, 3
4k + 3 – на 7, а
7
4k оканчивается на 1, 7
4k + 1 – на 7,
7
4k + 2 – на 9, 7
4k + 3 – на 3.
Значит 43
43 = 43
4 × 10 + 3 оканчивается на 7,
и 17
77 = 17
4 × 19 + 1 оканчивается на 7.
Задача 3:
Полторы курицы за полтора дня снесли полтора яйца. Сколько
яиц снесут 6 кур за 6 дней?
Решение:
Одна курица за полтора дня снесет 1 яйцо,
6 кур за полтора дня – 6 яиц
и 6 кур за 6 дней – 6 × 4 = 24 яйца.
Задача 4:
Постройте треугольник, середины
сторон которого будут в данных точках.
Решение:
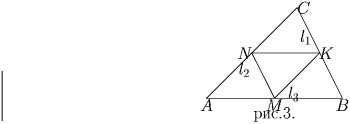
Пусть заданы M, N, K – середины сторон искомого
∆ ABC. (см. рисунок) Тогда MN || AC, NK || AB,
MK || BC. Отсюда способ построения ∆ ABC: через
точку K проводим прямую l
1 || MN, через точку N – l
2 || MK, и через точку M – l
3 || NK. Точки пересечения
этих прямых дадут вершины ∆ ABC, который, очевидно,
искомый. Задача имеет решение тогда и только тогда, когда точки M,
N, K не лежат на одной прямой.