Задача 2:
Сумма нескольких чисел равна 1. Может ли сумма их квадратов
быть мен 0.01?
Решение:
Да, может. Например, таким свойством обладает набор из 1000
чисел, каждое из которых равно 0.001.
Задача 3:
Даны шесть чисел 1,2,3,4,5,6.
Разрешается к любым двум числам добавлять единицу.
Можно ли все числа сделать равными?
Решение:
Нельзя. При одновременном добавлении единицы к любым двум числам
набора не может измениться чётность суммы всех чисел набора.
Изначальная сумма равна 21, а сумма любых шести равных целых
чисел чётна.
Задача 4:
Докажите, что для всех внутренних точек правильного пятиугольника
сумма расстояний до сторон одинакова.
(под расстоянием от точки до стороны пятиугольника понимается
расстояние от этой точки до прямой, содержащей данную сторону.)
Решение:
Пусть A
1A
2A
3A
4A
5 –
правильный пятиугольник со стороной a, O –
произвольная точка внутри его, h
1, h
2, … , h
5 –
расстояния от O
до прямых, содержащих стороны пятиугольника. Тогда
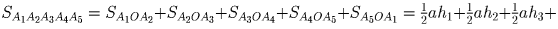
+ ½ah
4 + ½ah
5 = ½a(h
1 + h
2 + h
3 + h
4 + h
5).
Таким образом, сумма расстояний от O
до сторон пятиугольника равна
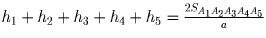
,
и не зависит от положения точки O.


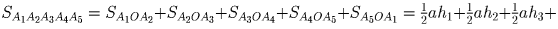 + ½ah4 + ½ah5 = ½a(h1 + h2 + h3 + h4 + h5).
Таким образом, сумма расстояний от O
до сторон пятиугольника равна
+ ½ah4 + ½ah5 = ½a(h1 + h2 + h3 + h4 + h5).
Таким образом, сумма расстояний от O
до сторон пятиугольника равна 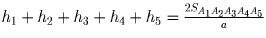 ,
и не зависит от положения точки O.
,
и не зависит от положения точки O.