 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVII олимпиада, 1996-1997 >> Заочный тур >> 9 класс | Убрать решения |
|
|
| XXXVII Екатеринбургская городская олимпиада, 1996-1997. Заочный тур. 9 класс |
|
|
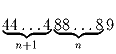 является точным квадратом для любого натурального числа n.
является точным квадратом для любого натурального числа n.Решение: Так как
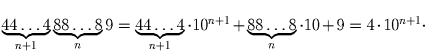
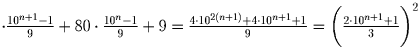 , доказательство сводится к проверке факта,
что число
, доказательство сводится к проверке факта,
что число 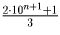 – целое. Но это очевидно,
так как сумма цифр числителя дроби равна 3.
– целое. Но это очевидно,
так как сумма цифр числителя дроби равна 3.Задача 2: Верно ли, что для любых натуральных чисел A, B и C найдется натуральное число K такое, что A + K делится на C, а A + B + K делится на C + 1? Решение: Да, верно. Рассмотрим число K = BC – A + mC(C + 1), где m – какое-нибудь натуральное число, достаточно большое, чтобы K было положительным. Тогда K + A = C(B + m(C + 1)) – делится на C, а K + A + B = (C + 1)(B + mC) – делится на C + 1. Натуральность K сомнений не вызывает. Задача 3: В городе n домов. Какое максимальное число непересекающихся заборов можно построить в этом городе, если каждый забор огораживает хотя бы один дом и никакие два забора не огораживают одну и ту же совокупность домов? Решение: Пусть φ (n) – наибольшее число заборов, ограждающих n домов.
2n – 1 забор построить всегда можно: занумеруем дома номерами от 1 до n и построим n заборов по правилу: i-ый забор огораживает совокупность домов с 1-го по i-ый. Ещё n – 1 получим, огораживая каждый дом в отдельности, начиная со второго. Доказано, что φ (n) ≥ 2n – 1.
Предположим, что φ (n) не всегда равно 2n – 1, и пусть n — наименьшее число с таким свойством. Ясно, что n ≠ 1. Построим φ (n) заборов в соответствии с требованиями задачи. Существует забор (назовём его внешним), огораживающий все дома. Выберем забор (I), отличный от внешнего и огораживающий наибольшее число домов – k. Тогда существует забор (II), огораживающий остальные n – k домов (следствие максимальности числа построенных заборов). Все остальные заборы находятся либо внутри I, либо внутри II. Имеем: φ (n) = φ (k) + φ (n – k) + 1. Так как и k, и n – k меньше n, φ (k) = 2k – 1 φ (n – k) = 2n – 2k – 1, поэтому φ (n) = 2n – 1 вопреки сделанному предположению.
Ответ: 2n – 1 забор.
Задача 4: Докажите равенство треугольников по трем медианам. Решение: Пусть AM, BN и CP – медианы треугольника ABC равные соответственно медианам A1M1, B1N1 и C1P1 треугольника A1B1C1. Продолжим медиану AM за точку M и отложим на ней отрезок MK = MO, где O – центр тяжести треугольника ABC. Проделаем аналогичное построение для треугольника A1B1C1 (см. рисунок).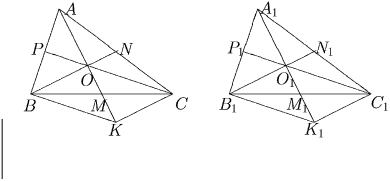
Четырёхугольник BOCK – параллелограмм, так как его диагонали делятся пополам точкой их пересечения, поэтому (учитывая свойство медиан делится в отношении 2:3 в точке пересечения) треугольник BOK подобен треугольнику, составленному из отрезков AM, BN и CP с коэффициентом подобия ⅔. То же верно и для треугольника B1O1K1. Тогда ∆ BOK = ∆ B1O1K1, поэтому BM = B1M1 как медианы в равных треугольниках, откуда BC = B1C1. Аналогично доказываются равенства AB = A1B1 и AC = A1C1.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVII олимпиада, 1996-1997 >> Заочный тур >> 9 класс | Убрать решения |