 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVIII олимпиада, 1997-1998 >> Областной тур >> 10 класс >> 2-й день | Убрать решения |
|
|
| XXXVIII Екатеринбургская городская олимпиада, 1997-1998. Областной тур. 10 класс. 2-й день |
|
|
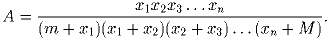
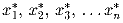 из отрезка
[m,M], при которых выражение A
принимает наибольшее значение. Сможете ли Вы найти эти числа?
из отрезка
[m,M], при которых выражение A
принимает наибольшее значение. Сможете ли Вы найти эти числа?Решение:
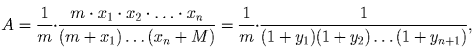
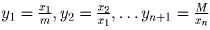 .
Обозначим буквой B выражение (1 + y1)(1 + + y2) … (1 + yn + 1).
Тогда исходная
задача эквивалентна следующей: найти наименьшее значение
выражения B при ограничениях:
.
Обозначим буквой B выражение (1 + y1)(1 + + y2) … (1 + yn + 1).
Тогда исходная
задача эквивалентна следующей: найти наименьшее значение
выражения B при ограничениях:
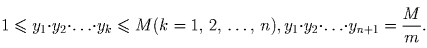
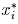 ,
решающие задачу Гюйгенса. По ним однозначно восстанавливаются числа
,
решающие задачу Гюйгенса. По ним однозначно восстанавливаются числа
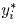 , решающие вторую задачу (и наоборот). Покажем, что все числа
, решающие вторую задачу (и наоборот). Покажем, что все числа
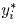 равны между собой. От противного, пусть для некоторого
номера i
равны между собой. От противного, пусть для некоторого
номера i 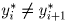 . Пусть
. Пусть 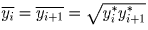 . Покажем, что при замене
. Покажем, что при замене 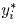 на
на
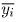 и
и 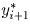 на
на 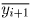 выражение
B уменьшится, и что числа
выражение
B уменьшится, и что числа 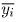 и
и 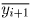 удовлетворяют ограничениям второй задачи. Отсюда будет следовать,
что числа
удовлетворяют ограничениям второй задачи. Отсюда будет следовать,
что числа 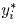 не реализуют минимум выражения B, то есть
противоречие с их выбором.
не реализуют минимум выражения B, то есть
противоречие с их выбором.Для доказательства первого утверждения достаточно проверить неравенство:
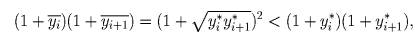
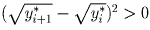 в силу того, что
в силу того, что 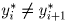 .
.Покажем, что числа 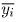 и
и 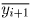 удовлетворяют указанным ограничениям. Возможны два случая:
удовлетворяют указанным ограничениям. Возможны два случая:
Случай i ≥ 2. Имеем:
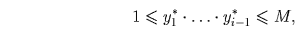
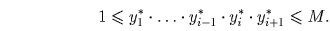
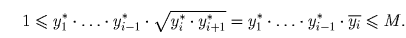
В случае i = 1 из неравенств 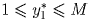 и
и 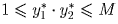 требуется вывести, что
требуется вывести, что 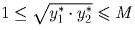 .
Левое неравенство здесь очевидно, а правое следует из
цепочки:
.
Левое неравенство здесь очевидно, а правое следует из
цепочки:
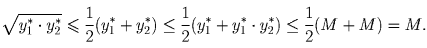
Итак, 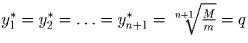 ,
,
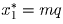 ,
, 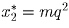 , … ,
, … , 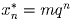 .
.
ОТВЕТ: 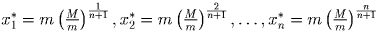 .
.
Задача 6: Докажите, что уравнение x² + y² = z³ имеет бесконечно много решений в натуральных числах.
Решение:
Будем искать решения в виде x = y = 2n,z = 2k. Тогда 22n + 22n = (2k)³. Получаем диофантово уравнение 2n + 1 = 3k. Так как n и k натуральные, то k нечётно, т.е. k = 2l – 1. Тогда 2n + 1 = 6l – 3,n = 3l – 2, и исходное уравнение имеет решения x = y = 23l – 2,z = 22l – 1 (l ∈ N).
Задача 7: Ортогональные проекции на плоскости всех граней треугольной пирамиды отрезка, соединяющего середины его противоположных рёбер, имеют равные длины. Докажите, что таким же свойством обладает и любой из двух других отрезков, соединяющих середины противоположных рёбер пирамиды.
(Н.Агаханов)
Решение:Покажем, что условие задачи эквивалентно тому, что в тетраэдре равны все высоты. (Ясно, что тогда вывод задачи будет очевиден). Пусть KM – отрезок, соединяющий середины рёбер BD и AC тетраэдра ABCD, причём MK1 = MK2 = KM1 = KM2, где K1 и K2 – проекции точки K на плоскости ABD и CBD, а M1 и M2 – проекции точки M на плоскости ACD и ABC (см. рис.24). Тогда прямоугольные треугольники KMK1,KMK2,KMM1,KMM2 с общей гипотенузой KM равны, следовательно, KK1 = KK2 = MM1 = MM2. Но эти отрезки — половины высот тетраэдра, значит, все высоты тетраэдра также равны. Наоборот, из равенства высот следует равенство отрезков KK1,KK2,MM1,MM2 (как их половин), равенство треугольников KMK1,KMK2,KMM1,KMM2 (по катету и гипотенузе), и, наконец, равенство проекций MK1 = MK2 = KM1 = KM2. Утверждение полностью доказано.
Задача 8: Есть три поля: на одном лежит стопка из n монет, два других свободны. За один ход можно переложить монету с верха любой стопки на свободное поле или на верх любой другой стопки. За какое наименьшее число ходов удастся собрать стопку в обратном порядке на том же поле?
(А.Шаповалов)
Решение:Покажем, как выполнить задание за 3n – 2 хода. Обозначим поля A B и C, причём стопка пусть лежит на A. Верхнюю монету перекладываем на B (1 ход), остальные – на C (n – 1 ходов), первую – обратно на A (1 ход), все с C, кроме нижней – на B (n – 2 ходов), нижнюю — на A (1 ход), наконец, все монеты с B на A (ещё n – 2 ходов). Всего 1 + (n – 1) + 1 + (n – 2) + 1 + (n – 2) = 3n – 2 хода.
Меньшим числом ходов обойтись нельзя. Предположим противное. Так как ни одна монета не может всё время оставаться на A, каждая из монет сделала не менее двух ходов. В силу принципа Дирихле есть три монеты сделавшие ровно по 2 хода, значит, по крайней мере две из них побывали на одном и том же поле B или C. Выбросим все остальные монеты и повторим в том же порядке ходы этих двух монет – выясняется, что изменить их порядок в стопке невозможно. Противоречие.
ОТВЕТ: 3n – 2 хода.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVIII олимпиада, 1997-1998 >> Областной тур >> 10 класс >> 2-й день | Убрать решения |