 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVIII олимпиада, 1997-1998 >> Областной тур >> 11 класс >> 1-й день | Убрать решения |
|
|
| XXXVIII Екатеринбургская городская олимпиада, 1997-1998. Областной тур. 11 класс. 1-й день |
|
|
Найти наибольшее значение a² + b² + c², если |ax² + bx + c| ≤ 1 для всех x ∈ [ – 1,\,1].
Решение: Подставив в данное неравенство значение x = 0, получим – 1 ≤ c ≤ 1 (откуда следует c² ≤ 1), а подставив значения x = 1 и x = – 1 – неравенства – 1 ≤ a + b + c ≤ 1 и – 1 ≤ a – b + c ≤ 1 соответственно. Умножим первое неравенство на – 1 и сложим его почленно со вторым и третьим. Получим неравенства |a + b| ≤ 2 и |a – – b| ≤ 2. Возведем их в квадрат (что допустимо, ибо обе части каждого из неравенств неотрицательны) и сложим. Имеем a² + b² ≤ 4, откуда a² + b² + c² ≤ 5. Легко проверяется, что равенство достигается при a = 2,b = 0,c = – 1 (или при a = – 2,b = 0,c = 1). Действительно, неравенство |2x² – 1| ≤ 1 поочередно эквивалентно неравенствам – 1 ≤ 2x² – 1 ≤ 1, 0 ≤ 2x² ≤ 2, x² ≤ 1 и, наконец, – 1 ≤ x ≤ 1, то есть оно верно при всех x ∈ [ – 1,\,1].
ОТВЕТ: 5.
Задача 2: Найдите два многочлена P(x) и Q(x) с целыми коэффициентами таких, что множество значений дробно-рациональной функции
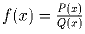 есть промежуток
есть промежуток 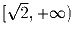 .
.
(В.Сендеров)
Решение:Будем искать 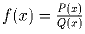 в виде
в виде 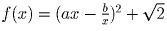 , где a и b – положительные числа. Ясно, что тогда область
значений f(x) – требуемый промежуток. Так как
, где a и b – положительные числа. Ясно, что тогда область
значений f(x) – требуемый промежуток. Так как 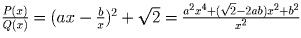 ,
достаточно выбрать a и b так, чтобы числа
,
достаточно выбрать a и b так, чтобы числа 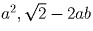 и b²
были рациональными. Это достигается, например, при
и b²
были рациональными. Это достигается, например, при 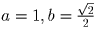 . Тогда
. Тогда 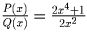 , а
искомые многочлены – P(x) = 2x4 + 1 и Q(x) = 2x².
, а
искомые многочлены – P(x) = 2x4 + 1 и Q(x) = 2x².
ОТВЕТ: P(x) = 2x4 + 1, Q(x) = 2x².
Задача 3:
На окружности, описанной вокруг треугольника ABC, отмечены точки A1, B1, C1 – середины дуг CAB, ABC и BCA соответственно. Докажите, что касательные к окружности в точках A1 и C1 и серединный перпендикуляр к отрезку BB1 пересекаются в одной точке.
(М.Сонкин)
Решение:Обозначим буквами x,y, и z cоответственно величины дуг
AB,BC и CA Тогда 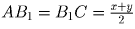 ,
,
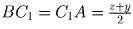 ,
,
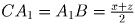 . Без ограничения общности положим, что
AB ≤ BC (см.рис.18). Тогда
. Без ограничения общности положим, что
AB ≤ BC (см.рис.18). Тогда 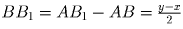 , поэтому
, поэтому
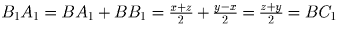 .
Но это означает, что точки C1 и A1 симметричны относительно
диаметра, проходящего через середину дуги BB1. Точка пересечения
касательных к окружности в точках A1 и C1 лежит на серединном
перпендикуляре к отрезку A1C1, который в силу установленной
симметрии совпадает с серединным перпендикуляром к отрезку BB1.
Доказательство завершено.
.
Но это означает, что точки C1 и A1 симметричны относительно
диаметра, проходящего через середину дуги BB1. Точка пересечения
касательных к окружности в точках A1 и C1 лежит на серединном
перпендикуляре к отрезку A1C1, который в силу установленной
симметрии совпадает с серединным перпендикуляром к отрезку BB1.
Доказательство завершено.
Задача 4:
В некоторой компании у каждых трёх человек имеется ровно один общий знакомый среди членов этой компании. Сколько человек может насчитывать такая компания?
Решение:Пусть в компании n человек. Ясно, что n ≥ 3 (иначе просто нет ни одной тройки), и что n ≠ 3 (в противном случае у трех человек, составляющих компанию, нет общего знакомого). Выберем произвольного члена компании, скажем A, и рассмотрим всевозможные тройки с его участием. У каждой такой тройки есть общий знакомый. Докажем, что у различных троек общие знакомые различны. Пусть, от противного B – общий знакомый троек A,C1,C2 и A,D1,D2. Пары C1C2 и D1D2 различны, поэтому из C1,C2,D1,D2 можно выбрать тройку. Но тогда у нее будет два общих знакомых — A и B – противоречие.
Общее количество рассматриваемых троек – 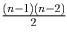 и по
доказанному оно не больше числа членов компании, отличных от A.
Имеем:
и по
доказанному оно не больше числа членов компании, отличных от A.
Имеем: 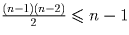 , откуда n ≤ 4. Случай n = 4
возможен: в компании 4 человека и все знают друг друга.
, откуда n ≤ 4. Случай n = 4
возможен: в компании 4 человека и все знают друг друга.
О Т В Е Т: в компании 4 человека.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVIII олимпиада, 1997-1998 >> Областной тур >> 11 класс >> 1-й день | Убрать решения |