 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVIII олимпиада, 1997-1998 >> Областной тур >> 11 класс >> 2-й день | Убрать решения |
|
|
| XXXVIII Екатеринбургская городская олимпиада, 1997-1998. Областной тур. 11 класс. 2-й день |
|
|
(Н.Агаханов)
Решение:Пусть многочлен Pn(x) = xn + a1xn – 1 + … + an – 1x + an удовлетворяет условиям задачи. Тогда он имеет по крайней мере 3 корня, поэтому n > 2. Если n нечётно, то при x → – ∞ Pn(x) → – ∞ , следовательно, условие Pn(x) > – 3 при всех x ∈ R не выполнено. Итак, n четно. Пусть n = 4, тогда Pn(x) = x4 + a1x³ + a2x² + a3x + a4. Подставляя значения x = 0 и x = ± 2, получаем: a4 = 0,16 ± 8a1 + 4a2 ± 2a3 = 0, откуда a2 = – 4,a3 = – 4a1, то есть Pn(x) = x4 + a1x³ – 4x² – 4a1x. Так как Pn(1) > – 3 имеем 1 + a1 – 4 – 4a1 > – 3, или a1 < 0. Так как Pn( – 1) > – 3 имеем 1 – a1 – 4 + 4a1 > – 3, или a1 > 0. Противоречие, показывающее, что n ≠ 4. Пусть n = 4 + 2k, где k – натуральное число. Тогда многочлен Pn(x) = (x – 2)²(x + 2)²x2k удовлетворяет, очевидно, всем условиям задачи.
ОТВЕТ: при всех четных n, больших 5.
Задача 6: Существуют ли 1998 нецелых рациональных чисел, произведение любых двух из которых – целое число?
(А.Малистов, А.Белов)
Решение:Да, существуют. Выберем различные простые числа pi (1 ≤ i ≤ 1998)
и положим 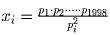 для всех
i. Все они не целые (числитель на знаменатель не делится), а
произведение любых двух xi • xj – произведение квадратов
выбранных простых чисел, кроме pi и pj, то есть целое число.
для всех
i. Все они не целые (числитель на знаменатель не делится), а
произведение любых двух xi • xj – произведение квадратов
выбранных простых чисел, кроме pi и pj, то есть целое число.
Задача 7: В пространстве расположены четыре попарно скрещивающиеся прямые. Докажите, что найдётся полуплоскость, границей которой является одна из этих прямых, не пересекающаяся с остальными тремя прямыми.
(Р.Карасёв)
Решение:Обозначим прямые l1, l2, l3 и l4.
Если все они параллельны некоторой плоскости α ,
то достаточно взять 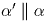 так, что
l1 и в качестве
полуплоскости одну из
полуплоскостей, на которые l1 делит
так, что
l1 и в качестве
полуплоскости одну из
полуплоскостей, на которые l1 делит 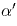 .
Иначе найдутся три прямые
(без ограничения общности l1,l2 и l3), которые не параллельны
одной плоскости.
Пусть α 12 – плоскость, параллельная l1 и l2 и такая, что l1
и l2 лежат
от неё по разные стороны. Аналогично определим плоскости α 13 и
α 23.
Обозначим X1 двугранный угол, который ограничен α 12, α 13 и содержит l1.
Аналогично определим X2 и X3. Заметим, что X1 и X2
не пересекаются
(они содержат l1 и l2, лежащие по разные стороны от α 12).
Аналогично
не пересекаются любые два из углов X1,X2 и X3.
.
Иначе найдутся три прямые
(без ограничения общности l1,l2 и l3), которые не параллельны
одной плоскости.
Пусть α 12 – плоскость, параллельная l1 и l2 и такая, что l1
и l2 лежат
от неё по разные стороны. Аналогично определим плоскости α 13 и
α 23.
Обозначим X1 двугранный угол, который ограничен α 12, α 13 и содержит l1.
Аналогично определим X2 и X3. Заметим, что X1 и X2
не пересекаются
(они содержат l1 и l2, лежащие по разные стороны от α 12).
Аналогично
не пересекаются любые два из углов X1,X2 и X3.
Рассмотрим угол X1. Так как l2 и l3 не пересекают его, а l1 в нём содержится, то любая полуплоскость с краем l1, лежащая в этом угле, не пересекает l2 и l3. Что же касается l4, то она может помешать проведению полуплоскости через l1 в угле X1 только если она пересекает X1 по отрезку. Аналогично, рассуждая от противного, l4 пересекает X2 и X3 по отрезкам, но это значит, что три плоскости α 12, α 13 и α 23 высекают на прямой l4 три отрезка, что невозможно (три точки разделяют прямую на 2 отрезка и 2 луча). Противоречие, показывающее, что требуемую полуплоскость через какую-то из прямых l1,l2,l3 провести можно.
Задача 8: Поле для игры в бильярд имеет размеры m × n дюймов (m,n — натуральные числа). Разрешается установить шар в любую точку поля, отстоящую от бортов на целое число дюймов, и нанести по нему удар под углом 45° к любому из бортов. Угол падения равен углу отражения; при попадании в угол поля шар отскакивает в противоположном направлении. Сколько различных траекторий может получиться в зависимости от m и n?
Решение:
ОТВЕТ: (n,m) + 1 траекторий, где (n,m) – наибольший общий делитель чисел m и n.
1 способ. Назовём траектории, проходящие через угол поля, траекториями первого типа, а остальные – траекториями второго типа. Так как каждая траектория либо не проходит через углы, либо проходит ровно через два угла, то существует ровно 2 траектории первого типа. Выпустим шар из произвольной точки поля и засечём момент, когда он впервые вернётся в исходную точку, а направление его скорости совпадёт с первоначальным. Тогда если шар двигался по траектории первого типа, он прошёл её дважды (туда и обратно), а если по траектории второго типа – то ровно один раз.
Найдём длину пути, пройденного шаром. Для этого рассмотрим
движение шара в проекции на борт поля, длина которого m дюймов.
Очевидно, что в этой проекции шар совершает возвратно-поступательные
движения с амплитудой m. Чтобы шар оказался в первоначальной
точке с первоначально направленной скоростью, он должен полностью
пройти путь туда – обратно целое число раз, скажем, k. Тогда
длина пройденного шаром пути в проекции равна km, а реально
путь шара равен 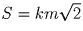 .
Аналогично рассмотрим движение шара в проекции
на другой борт. Получим, что путь шара равен
.
Аналогично рассмотрим движение шара в проекции
на другой борт. Получим, что путь шара равен 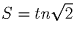 для
некоторого натурального
t. Так как S одно и то же, имеем уравнение в
натуральных числах tn = km, причём числа t и k – наименьшие,
удовлетворяющие такому уравнению (так как шар впервые вернулся
в исходную точку с начальной скоростью). Тогда tn —
наименьшее общее кратное чисел n и m (обозначим его НОК),
и оно не зависит от
начального положения шара, то есть длина любой траектории второго
типа равна S.
для
некоторого натурального
t. Так как S одно и то же, имеем уравнение в
натуральных числах tn = km, причём числа t и k – наименьшие,
удовлетворяющие такому уравнению (так как шар впервые вернулся
в исходную точку с начальной скоростью). Тогда tn —
наименьшее общее кратное чисел n и m (обозначим его НОК),
и оно не зависит от
начального положения шара, то есть длина любой траектории второго
типа равна S.
Пусть траекторий второго типа x, тогда
суммарная длина всех траекторий равна 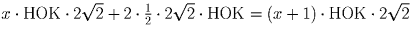 .
С другой стороны, в каждой«единичной" клеточке поля проходят
ровно 2 участка траекторий длины
.
С другой стороны, в каждой«единичной" клеточке поля проходят
ровно 2 участка траекторий длины 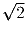 каждый, поэтому
суммарная длина траекторий равна
каждый, поэтому
суммарная длина траекторий равна 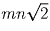 .
.
Имеем уравнение: 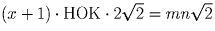 ,
откуда
,
откуда 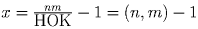 (здесь (n,m) —
наибольший общий делитель чисел n и m). Тогда общее число траекторий
равно
x + 2 = (n,m) + 1.
(здесь (n,m) —
наибольший общий делитель чисел n и m). Тогда общее число траекторий
равно
x + 2 = (n,m) + 1.
2 способ.
1) На квадратном поле n × n любая траектория – суть либо дважды пройденная диагональ, либо прямоугольник со сторонами, параллельными диагоналям поля (см.рис.25). Таким образом, число траекторий на таком поле равно n + 1.
2) Пусть поле имеет размеры m × n, где m > n. Покажем, что если от него отделить квадратный кусок n × n, то количество траекторий на укороченном поле не изменится. Проведём на поле прямую, отделяющую от него квадрат n × n, и рассмотрим произвольную траекторию. Если эта траектория пересекает проведённую линию во внутренней точке, скажем, в M (см. рис. 26, траектория I), то далее шар движется по границе некоторого прямоугольника (см. пункт 1) и возвращается в M. Если же траектория проходит через точку пересечения проведённой прямой с одним из бортов (траектория II), то шар попадает в угол поля и затем возвращается по той же самой траектории. В обоих случаях шар ведёт себя так, как если бы вместо проведённой прямой был жёсткий барьер (борт поля). Таким образом, каждой траектории на поле m × n соответствует траектория на поле (m – n) × n (получаемая путём отсечения части изначальной траектории, которая лежит в квадрате n × n), и наоборот. Утверждение доказано.
3) В силу доказанного в пункте 2, если m = kn + t, где 1 ≤ t ≤ n, число траекторий на полях размера m × n и n × t одно и то же. Повторяя эту операцию несколько раз, придём к квадратному полю размера d × d, где d – наибольший общий делитель чисел m и n. По первому пункту, число траекторий на таком поле d + 1.
Замечание. По сути дела в пункте 3 осуществлён алгоритм Евклида для нахождения наибольшего общего делителя чисел m и n.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVIII олимпиада, 1997-1998 >> Областной тур >> 11 класс >> 2-й день | Убрать решения |