 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVIII олимпиада, 1997-1998 >> Областной тур >> 7 класс >> 1-й день | Убрать решения |
|
|
| XXXVIII Екатеринбургская городская олимпиада, 1997-1998. Областной тур. 7 класс. 1-й день |
|
|
Решение:
S(a) Π (a) = 1998 = 2 • 3 • 3 • 3 • 37.
Так как 37 – простое число, то либо S(a) либо
Π (a) делится на 37, а так как Π (a) – произведение
цифр и потому на 37 не делится, S(a) = 37k. Число a тем меньше, чем
меньше цифр в его записи, поэтому k = 1, то есть S(a) = 37, Π (a) = 54.
Представить произведение наименьшим числом цифр можно только так: 54 = 6 • 9, а получить S(a) = 37 можно только с помощью 22 единиц, значит,
минимальное искомое число 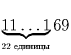 .
.
Задача 2: Даны 7 попарно пересекающихся прямых на плоскости. Известно, что любые три прямые пересекаются в одной точке. Докажите, что все прямые пересекаются в одной точке.
Решение:
Занумеруем прямые цифрами от 1 до 7. Возьмем прямые 1, 2 и 3 – они пересекаются в одной точке, скажем, в точке A. Затем возьмем прямые 1, 2, 4. Они также пересекаются в A, так как прямые 1 и 2 имеют только одну точку пересечения. Аналогично, получаем, что прямые 5, 6 и 7 также проходят через A.
Задача 3: Имеется семь монет, из которых две фальшивые, весящие меньше настоящих на 1 грамм. За три взвешивания на чашечных весах без гирь определите обе фальшивые монеты.
Решение:
Занумеруем монеты цифрами от 1 до 7. Первым взвешиванием сравним монеты 1, 2, 3 и 4, 5, 6. Возможны два случая.
Случай 1: Весы в равновесии. Тогда на каждой чашке весов по одной фальшивой монете. Вторым взвешиванием выделим фальшивую монету из группы 1, 2, 3, для чего сравним монеты 1 и 2. Если их веса равны, то фальшивая монета 3, если неравны, то фальшивая та, которая легче. Третьим взвешиванием аналогично находим вторую фальшивую монету.
Случай 2: Одна из групп (скажем, 1, 2, 3) перевесила. Тогда обе фальшивые монеты в группе 4, 5, 6, 7. Вторым взвешиванием сравним монеты 4 и 5. Если их веса различны, то более легкая — фальшивая, и тогда последним взвешиванием (например, сравнивая монеты 6 и 7) находим и вторую фальшивую. Если веса равны, то фальшивые монеты либо 4 и 5, либо 6 и 7. Сравним третьим взвешиванием монеты 4 и 6, и узнаем какой из этих случаев имеет место.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVIII олимпиада, 1997-1998 >> Областной тур >> 7 класс >> 1-й день | Убрать решения |