Задача 1: В полдень из пункта А в пункт Б выехал «Москвич». Одновременно из Б в А по той же дороге выехали «Жигули». Через час «Москвич» находился на полпути от А до «Жигулей». Когда он окажется на полпути от «Жигулей» до Б? (Скорости автомобилей постоянны).

(С.Токарев)

Решение: Пусть S — расстояние между пунктами A и Б,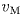  — скорость«Москвича",  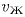— скорость«Жигулей", t — время от начала движения, когда«Москвич" окажется на полпути от "Жигулей" до B, x — расстояние между«Москвичом" и пунктом Б через t от начала движения.

Тогда через час от начала движения

.

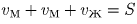Через t от начала движения

,

.

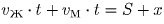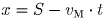Откуда 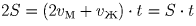, а значит t = 2.

Задача 2: На гранях куба написаны натуральные числа, а в каждой вершине — произведение чисел на трёх гранях с этой вершиной. Найдите сумму чисел на гранях, если сумма в вершинах равна 70.

(А.Шаповалов)

Решение: Пусть n₁, n₂, n₃, n₄, n₅, n₆ — числа на гранях куба. Тогда n₅(n₁n₄ + n₁n₂ + n₂n₃ + n₃n₄) + n₆(n₁n₄ + n₁n₂ + n₂n₃ + n₃n₄) = (n₅ + n₆)(n₁(n₄ + n₂) + n₃(n₂ + n₄)) = (n₅ + n₆)(n₄ + n₂)(n₁ + n₃) = 70 = 7 • 5 • 2 • 1. Так как числа натуральные, то n_i + n_j > 1, и, следовательно, (n₅ + n₆) + (n₄ + n₂) + (n₁ + n₃) = 7 + 5 + 2 = 14.

Задача 3: На стороне BC треугольника ABC выбрана точка F. Оказалось, что отрезок AF пересекает медиану BD в точке E так, что AE = BC. Докажите, что BF = FE.

(М.Сонкин)

Решение: На продолжении медианы BD отложим DE₁ = DE (см. рис.14). Тогда  ∆ ADE =  ∆ CDE₁ по I признаку равенства треугольников (AD = DC, DE₁ = DE,  ∠ ADE =  ∠ CDE₁ как вертикальные). Из равенства треугольников следует равенство соответствующих углов и соответствующих сторон:  ∠ AED =  ∠ DE₁C, E₁C = AE = BC. Значит  ∆ BCE₁ — равнобедренный, и  ∠ DE₁C =  ∠ EBC.  ∠ AED =  ∠ BEF, как вертикальные, то  ∠ EBF =  ∠ BEF, и  ∆ BFE — равнобедренный.

Задача 4: Барон Мюнгхаузен покупает перчатки первого, второго и третьего размеров. В магазине имеется 300 перчаток – по 100 штук каждого из указанных размеров. Правых и левых перчаток поровну, то есть, по 150 штук. Барон утверждает, что он может выбрать по меньшей мере 50 пар перчаток (в каждой паре – левая и правая перчатки одного размера), хотя продавец возражает против этого. Прав ли барон?

Решение: Обозначим соответственно через x₁, x₂, — левые и правые перчатки I сорта, через y₁, y₂ — левые и правые перчатки II сорта и через z₁, z₂ — левые и правые перчатки III сорта. Пусть x = minx₁,x₂, y = miny₁,y₂, z = minz₁,z₂.

Барон утверждает, что x + y + z ≥ 50.

Если хотя бы одно из чисел x₁, y₁ и z₁ равно 50, то утверждение барона справедливо.

Если все числа x₁, y₁ и z₁ отличны от 50, тогда из условия x₁ + y₁ + z₁ = 150 следует, что x₁, y₁ и z₁ не могут быть одновременно больше 50 и не могут быть одновременно меньше 50. Без ограничения общности будем считать, чтоx₁ < 50, y₁ < 50иz₁ > 50 (в противном случае можно будет провести аналогичные рассуждения относительно x₂, y₂ и z₂). Тогда x = x₁, y = y₁, z = z₂ и x + y + z = (x₁ + y₁) + z₂ = (150 – z₁) + (100 – z₁) = 250 – 2z₁. Если x + y + z < 50, то 250 – 2z₁ < 50, и z₁ > 100. Противоречие. Следовательно, x + y + z ≥ 50, значит, барон прав.