 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVIII олимпиада, 1997-1998 >> Областной тур >> 8 класс >> 2-й день | Убрать решения |
|
|
| XXXVIII Екатеринбургская городская олимпиада, 1997-1998. Областной тур. 8 класс. 2-й день |
|
|
(А.Шаповалов)
Решение:Пусть найдутся 4 натуральных числа, удовлетворяющих условию. Так как из 6 последовательных чисел ровно 2 делятся на 3 (*), то найдутся 2 различные пары (a,b) и (c,d) такие, что наибольший общий делитель каждой пары делится на 3. Если все числа составляющие эти 2 пары различные, то тогда наибольший общий делитель каждой из 6 пар делится на 3. Противоречие с (*). Если у этих 2 пар совпадают два числа (допустим a = c), то тогда мы можем указать еще одну пару (b,d), отличную от исходных двух, наибольший общий делитель которой делится на 3. Противоречие с (*).
Задача 6: Проверьте следующее равенство:
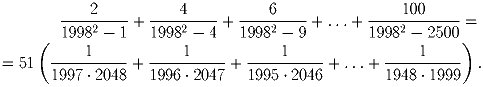
Решение:
Преобразуем левую часть равенства
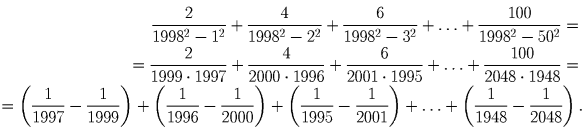
Преобразуем правую часть равенства
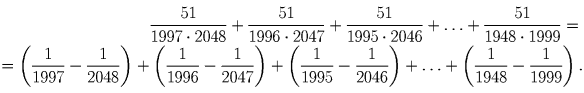
Так как левая часть равенства равна правой, то равенство справедливо.
Задача 7: В треугольнике ABC проведены биссектрисы AA1 и CC1. Докажите, что если длины перпендикуляров, опущенных из вершины B на прямые AA1 и CC1 равны, то треугольник ABC — равнобедренный.
(Н.Агаханов)
Решение:Пусть F и K точки пересечения перпендикуляров, опущенных из вершины B на прямые AA1 и CC1 соответственно, а O — точка пересечения биссектрис ∆ ABC (см. рис.21).
1) ∆ OKB = ∆ OFB (по катету и гипотенузе: BK = BF, OB — общая). Из равенства треугольников следует равенство соответствующих углов: ∠ KOB = ∠ FOB.
2) ∆ OBC1 = ∆ OBA1 по II признаку равенства треугольников (OB — общая, ∠ OBC1 = ∠ OBA1, так как OB — биссектриса ∆ ABC, ∠ KOB = ∠ FOB) Из равенства треугольников следует равенство соответствующих сторон: OC1 = OA1.
3) ∆ OAC1 = ∆ OCA1 по II признаку равенства треугольников (OC1 = OA1, ∠ C1OA = ∠ A1OC как вертикальные, ∠ AC1O = ∠ CA1O как смежные углы к равным углам равных треугольников ∆ OBC1 и ∆ OBA1) Из равенства треугольников следует равенство соответствующих углов: ∠ OAC1 = ∠ OCA1. Но ∠ OAC1 = ½ ∠ A, ∠ OCA1 = ½ ∠ C, откуда ∠ A = ∠ C, а значит ∆ ABC — равнобедренный.
Задача 8: Прожектор освещает развёрнутый угол (180). Можно ли расположить 19 прожекторов так, чтобы никакие 3 из них не находились на одной прямой и каждый прожектор освещал бы только один другой прожектор?
(Т.Емельянова)
Решение:Можно. Например, сначала расположить все прожекторы на окружности в точках P1,P2, … P19, так, чтобы все дуги были равны PiPi + 1 = 2 π /19 и так, чтобы развернутый угол, который освещает каждый прожектор, был перпендикулярен радиусу окружности в точке Pi и не освещал окружность. Затем каждый развернутый угол в точке Pi повернуть по часовой стрелке так, чтобы луч из Pi проходил через середину дуги Pi + 1Pi + 2.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVIII олимпиада, 1997-1998 >> Областной тур >> 8 класс >> 2-й день | Убрать решения |