 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVIII олимпиада, 1997-1998 >> Областной тур >> 9 класс >> 2-й день | Убрать решения |
|
|
| XXXVIII Екатеринбургская городская олимпиада, 1997-1998. Областной тур. 9 класс. 2-й день |
|
|
(А.Шаповалов)
Решение:По теореме Виета c = ax1x2, b = – a(x1 + x2). Предположим, что среди рассматриваемых чисел нет нуля, и m – наименьший из модулей этих чисел. Тогда |c| = |a| • |x1| • |x2| ≥ 1 • 2 • 3 = 6. Отсюда m ≥ 2, но |c| > m³, значит разность между c и наименьшим по модулю числом больше 4 – противоречие. Итак, среди чисел есть 0. Так как двух нулей быть не может, из равенства c = ax1x2 находим, что b = 0. Тогда сумма корней – 0, разность не больше 4, то есть корни либо 1 и -1, либо 2 и -2. В первом случае a = – c, и так как a и c соседние с 1 или -1, получаем ответы: 2x² – 2 и – 2x² + 2. Во втором случае c = – 4a, и разница между a и c больше 4, что невозможно.
ОТВЕТ: 2x² – 2 и – 2x² + 2.
Задача 6: Известно, что уравнение x³ + y³ = z³ не имеет решений в натуральных числах. Найдите все решения в натуральных числах уравнения 6x² + 2 = z³.
Решение:
Запишем уравнение в виде (x + 1)³ – (x – 1)³ = z³, откуда (x + 1)³ = (x – 1)³ + z³. В натуральных числах x + 1,x – 1 и z это уравнение решений не имеет (это дано в условии). Так как и z и x (а значит, и x + 1) должны быть натуральными, единственно возможный случай x – 1 = 0, то есть x = 1. Тогда z = 2.
ОТВЕТ: единственная пара x = 1, z = 2.
Задача 7: В треугольнике ABC, вписанном в окружность, AB < AC. На стороне AC отмечена точка D так, что AD = AB. Докажите, что серединный перпендикуляр к отрезку DC делит пополам дугу BC, не содержащую точки A.
(М.Сонкин)
Решение:Продолжим сторону BD до пересечения с описанной окружностью в точке E (см. рис.22). Треугольники ABD и CDE подобны (углы ∠ ABD и ∠ DCE равны, как вписанные, опирающиеся на одну и ту же дугу AE, а углы BDA и CDE равны, как вертикальные). Тогда DE = EC, а следовательно серединный перпендикуляр к отрезку DC является и биссектрисой угла E, поэтому делит дугу BC пополам.
Задача 8: Найдите наибольшее число l такое, что при любой раскраске единичного квадрата в 2 цвета внутри него найдётся отрезок с одноцветными вершинами длины не меньше, чем l.
(Л.Емельянов)
Решение:Покажем сначала, что при любой раскраске единичного квадрата в два
цвета найдутся две одноцветные точки, расстояние между которыми не
меньше 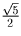 . Предположим, что при некоторой
раскраске таких точек нет.
Возьмём вершины A,B,D и середины E и F сторон
BC и DC соответственно (см.рис.23). Тогда точки E и F окрашены в
другой цвет, чем вершина A, точки B и F (как и точки D и E)
окрашены в разные цвета, поэтому цвет вершин B и D совпадает
с цветом вершины A. Но
. Предположим, что при некоторой
раскраске таких точек нет.
Возьмём вершины A,B,D и середины E и F сторон
BC и DC соответственно (см.рис.23). Тогда точки E и F окрашены в
другой цвет, чем вершина A, точки B и F (как и точки D и E)
окрашены в разные цвета, поэтому цвет вершин B и D совпадает
с цветом вершины A. Но 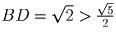 – противоречие.
– противоречие.
Покажем теперь как покрасить квадрат в два цвета, чтобы не было
одноцветных точек на расстоянии меньшем, чем 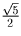 .
Проведём в
квадрате среднюю линию и раскрасим получившиеся два
прямоугольника каждый в свой цвет (точки средней линии при этом
можно раскрасить произвольным образом). Любые одноцветные точки
при этом лежат в одном из прямоугольников, а значит расстояние
между ними не превосходит диагонали прямоугольника, равной
.
Проведём в
квадрате среднюю линию и раскрасим получившиеся два
прямоугольника каждый в свой цвет (точки средней линии при этом
можно раскрасить произвольным образом). Любые одноцветные точки
при этом лежат в одном из прямоугольников, а значит расстояние
между ними не превосходит диагонали прямоугольника, равной
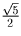 .
.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVIII олимпиада, 1997-1998 >> Областной тур >> 9 класс >> 2-й день | Убрать решения |