 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVIII олимпиада, 1997-1998 >> Районный тур >> 10 класс | Убрать решения |
|
|
| XXXVIII Екатеринбургская городская олимпиада, 1997-1998. Районный тур. 10 класс |
|
|
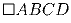 , причем
∠ BAM = 30, и ∠ BCM = 15.
Найти ∠ MDA.
, причем
∠ BAM = 30, и ∠ BCM = 15.
Найти ∠ MDA.Решение:
На прямой AM построим точку M′ такую, что ∠ M′DA = 60, и докажем, что точки M и M′ совпадают. ∆ AM′D — равносторонний, поэтому ∠ AM′D = 60, и M′D = AD = CD и, следовательно, ∆ M′DC – равнобедреный с углами ∠ M′DC = 30, ∠ CM′D = ∠ DCM′ = 75. Поэтому ∠ M′CB = 15, и в силу определения точки M получаем, что M = M′.
Ответ: ∠ MDA = 60.
Задача 2: Пусть числа a,b,c удовлетворяют неравенствам a + b + c > 0,ab + ac + bc > 0,abc > 0.
Доказать, что a > 0,b > 0,c > 0.
Решение:
Так как abc > 0, то либо a > 0,b > 0,c > 0, либо среди чисел a,b,c
одно положительное и два
отрицательных. Например, a > 0,b < 0, c < 0. Покажем,
что такое невозможно. Действительно, тогда a > – b – c,bc > a( – b – c) > ( – b – c)², так как a > 0, – b – c > 0.
Отсюда bc > b² + 2bc + c², то есть b² + bc + c² < 0.
Но  . —
противоречие. Следовательно, a > 0,b > 0,c > 0.
. —
противоречие. Следовательно, a > 0,b > 0,c > 0.
Задача 3: Натуральные числа a,b,c таковы, что a² + b² + c² делится на ab + bc + ca, а число a + b + c – простое.
Докажите, что a = b = c = 1.
Решение:
Обозначим
 тогда
тогда

Задача 4: 15 команд играют турнир в один круг.
Докажите, что в некотором матче встретятся команды, сыгравшие перед этим в сумме нечетное число матчей.
Решение: Допустим противное. Тогда если одна из двух встречающихся в матче команд сыграла до матча четное число игр, то другая – тоже (назовем такие матчи четными). Каждая команда сыграла по 7 четных матчей, поэтому удвоенное (в матче участвуют две команды) число четных матчей равно 7 × 15, но это число – нечетное. Противоречие.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVIII олимпиада, 1997-1998 >> Районный тур >> 10 класс | Убрать решения |