 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVIII олимпиада, 1997-1998 >> Районный тур >> 7 класс | Убрать решения |
|
|
| XXXVIII Екатеринбургская городская олимпиада, 1997-1998. Районный тур. 7 класс |
|
|
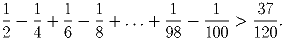
Решение:

(Воспользовались тем, что разность дробей в каждой скобке положительна.)
Задача 2: Точка B лежит на отрезке AC; AB = 2, BC = 1.
Указать на прямой AB все точки M, для которых AM + MB = CM.
Решение: Пусть точки A,B,C имеют координаты 0, 2 и 3 соответственно. Пусть координата точки M равна x.
Так как  ,
,  ,
,  , то приходим к уравнению
, то приходим к уравнению  , решая которое получаем два ответа: x = 1 и x = – 1.
, решая которое получаем два ответа: x = 1 и x = – 1.
Задача 3: В классе 30 человек. Только двое из них не любят ни математику, ни физику, ни биологию. 14 учеников любят математику, 15 – физику, 11 – биологию, 6 – физику и математику, 5 –физику и биологию и 3 – математику и биологию.
Сколько учащихся любят сразу 3 указанных предмета?
Решение:
Пусть количество учащихся, которые любят все три предмета, равно x. На математической модели задачи – кругах Эйлера – получаем следующую«картину" (см. рис.1.).
Теперь очевидно, что количество любителей только математики равно 14 – (3 – x + x + 6 – x) = 5 + x, только физики – (15 – (5 – x + x + 6 – x)) = 4 + x, только биологии – (11 – (3 – x + x + 5 – x)) = 3 + x. Получаем уравнение 5 + x + 4 + x + 3 + x + x + 3 – x + 5 – x + 6 – x = 28, откуда x = 2.
Задача 4: У продавца имеется 10 гирь весом 1, 2, 3, …10 кг. Известно, что все покупатели, стоящие в очереди к продавцу, купили разное целое число килограммов товара. Какое максимальное число покупателей могло стоять в очереди?
Решение:
Составим следующую таблицу:

Из таблицы видно, что максимально возможное число килограммов у покупателя может быть 55. Покажем, что число покупателей не меньше 55.
Действительно, пусть x – целое число килограммов товара и такое, что 1 ≤ x ≤ 55. Тогда x заключено между двумя последовательными числами нижней строки таблицы. Эти числа выражаются как сумма килограммов всех гирь, отмеченных в колонках, соответствующих этим числам. Но от одного числа к другому можно перейти, вычитая последовательно из большего числа 1, 2 и т.д., т.е. все числа, записанные в виде элементов суммы в верхней строке колонки, соответствующей большeму числу.
Например, если 45 ≤ x ≤ 55, то в верхней строке для 55 стоит сумма 1 + 2 + 3 + … + 10. Вычитая из 55 единицу, двойку и т.д., получаем, соответственно, 54,53, … 45. Таким образом, любое число x, такое, что 1 ≤ x ≤ 55, может быть представлено в виде набора чисел от 1 до 10, взятых по одному разу. Следовательно, 55 человек могло стоять в очереди у продавца.
Ответ. 55 человек.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVIII олимпиада, 1997-1998 >> Районный тур >> 7 класс | Убрать решения |