 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVIII олимпиада, 1997-1998 >> Заочный тур >> 10 класс | Убрать решения |
|
|
| XXXVIII Екатеринбургская городская олимпиада, 1997-1998. Заочный тур. 10 класс |
|
|

Решение:
Пусть x² + x + 1 = t. Тогда t² = x²(t + 2x²), откуда t1 = 2x²,t2 = – x².
Уравнение 2x² + x + 1 = 0 решений не имеет, а из уравнения x² – x – 1 = 0
получаем ответ:  .
.
Ответ:  .
.
Задача 2: Докажите, что среди 18 последовательных трехзначных натуральных чисел найдется хотя бы одно, которое делится на сумму своих цифр.
Решение:
Среди трёхзначных чисел, делящихся на 9, только у числа 999 сумма цифр 27 (заметим, что 999 нечётное), а у остальных чисел указанного вида сумма цифр 9 или 18 (по признаку деления на 9). Рассмотрим 18 последовательных трёхзначных натуральных чисел. Среди них ровно 2 делятся на 9. Обозначим их k и k + 9. Выберем из них чётное (такое, очевидно, найдётся), тогда оно делится и на 9, и на 18, то есть на сумму своих цифр. Утверждение, сформулированное в задаче доказано.
Задача 3: В выпуклый четырехугольник вписан параллелограмм, вершины которого делят стороны четырехугольника в постоянном отношении 1:4 (считая по часовой стрелке).
Докажите, что исходный четырехугольник – тоже параллелограмм.
Решение:
Рассмотрим векторы  и пусть E,\,F,\,G,\,H – точки на сторонах
четырёхугольника ABCD, указанного в условии (см.рис.12).
Имеем:
и пусть E,\,F,\,G,\,H – точки на сторонах
четырёхугольника ABCD, указанного в условии (см.рис.12).
Имеем:

 ,
,
 ,
,
 ,
,
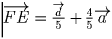 .
Решая систему, получаем
.
Решая систему, получаем  . Следовательно, ABCD —
параллелограмм.
. Следовательно, ABCD —
параллелограмм.Задача 4: Управдом Остап Бендер собрал с жильцов дома деньги на установку новых квартирных номеров. Адам Козлевич заинтересовался, почему у них в третьем подъезде надо собрать денег на 20 процентов больше, чем во втором, хотя квартир во всех подъездах поровну. Не растерявшись, Остап объяснил, что за двузначные номера приходится платить вдвое, а за трехзначные – втрое больше, чем за однозначные.
Сколько квартир в подъезде?
Решение:
Пусть x – число квартир в подъезде, а однозначный номер стоит s рублей. Поскольку в доме есть трёхзначные номера (они упомянуты) и нет четырёхзначных (они не упомянуты), то число 3x — трёхзначно, поэтому x – двузначно. Рассмотрим два случая:
1) Пусть число 2x – двузначно. Тогда во втором подъезде все номера двузначны, поэтому собрано 2xs руб. В третьем подъезде (99 – 2x) двузначных номеров и 3x – 99 трёхзначных, поэтому в нём собрано 2s(99 – 2x) + 3s(3x – 99) руб. По условию 1,2 • 2sx = 2s(99 – 2x) + 3s(3x – 99), откуда 2,4x = 5x – 99 и x – не целое.
2) Пусть число 2x – трёхзначно. Тогда во втором подъезде (99 – 2x) двузначных и (3x – 99) трёхзначных номеров, а в третьем – x трёхзначных номеров, откуда 1,2(4x – – 99) = 3x, и x = 66. Проверка показывает, что 2x и 3x действительно трёхзначны.
Ответ: 66 квартир.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVIII олимпиада, 1997-1998 >> Заочный тур >> 10 класс | Убрать решения |