 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVIII олимпиада, 1997-1998 >> Заочный тур >> 11 класс | Убрать решения |
|
|
| XXXVIII Екатеринбургская городская олимпиада, 1997-1998. Заочный тур. 11 класс |
|
|
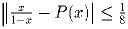 для всех x ∈ [0;½].
для всех x ∈ [0;½].Решение:
Подойдет, например, многочлен P(x) = x³ + x² + x. В самом деле,
 . При 0 ≤ x ≤ ½
функции x4 и
. При 0 ≤ x ≤ ½
функции x4 и  неотрицательны, монотонно возрастают, поэтому
функция
неотрицательны, монотонно возрастают, поэтому
функция  также монотонно возрастает. Для всех x ∈ [0;½] тогда имеем:
также монотонно возрастает. Для всех x ∈ [0;½] тогда имеем:  ,
что и требуется.
,
что и требуется.
Задача 2: Натуральные числа M и K отличаются перестановкой цифр. Доказать, что
а) сумма цифр чисел 2M и 2K одинакова;
б) сумма цифр чисел 5M и 5K одинакова.
Решение:
Обозначим через S(A) сумму цифр числа A. Пусть  ,
,  (числа 2ai и 5ai, очевидно, двузначные или однозначные).
Заметим, что bi ≤ 1,
ci – 1 ≤ 8, поэтому
bi + ci – 1 ≤ 9. Кроме того, ki ≤ 4, pi – 1 – либо 0, либо 5,
поэтому ki + pi – 1 ≤ 9. Тогда
2M = 2(10nan + 10n – 1an – 1 + … + 10a1 + a0) = 10n(10bn + + cn) + 10n – 1(10bn – 1 + cn – 1) + … + 10(10b1 + c1) + 10b0 + c0 = 10n + 1bn + 10n(bn – 1 + cn) + … + + 10(b0 + c1) + c0, причем bn,(bn – 1 + cn), … (b0 + c1),c0
— цифры числа 2M. Тогда S(2M) = bn + (bn – 1 + cn) + … + (b0 + c1) + c0 = (bn + cn) + (bn – 1 + cn – 1) + … + (b1 + c1) + (b0 + c0) = S(2an) + S(2an – 1) + … + S(2a0). Аналогично, 5M = 10n + 1kn + 10n(kn – 1 + pn) + … + + 10(k0 + p1) + p0, S(5M) = S(5an) + S(5an – 1) + … + S(5a0).
Очевидно, и S(2M), и S(5M) не зависит от порядка цифр ai в числе M,
поэтому S(2M) = S(2K), и S(5M) = S(5K).
(числа 2ai и 5ai, очевидно, двузначные или однозначные).
Заметим, что bi ≤ 1,
ci – 1 ≤ 8, поэтому
bi + ci – 1 ≤ 9. Кроме того, ki ≤ 4, pi – 1 – либо 0, либо 5,
поэтому ki + pi – 1 ≤ 9. Тогда
2M = 2(10nan + 10n – 1an – 1 + … + 10a1 + a0) = 10n(10bn + + cn) + 10n – 1(10bn – 1 + cn – 1) + … + 10(10b1 + c1) + 10b0 + c0 = 10n + 1bn + 10n(bn – 1 + cn) + … + + 10(b0 + c1) + c0, причем bn,(bn – 1 + cn), … (b0 + c1),c0
— цифры числа 2M. Тогда S(2M) = bn + (bn – 1 + cn) + … + (b0 + c1) + c0 = (bn + cn) + (bn – 1 + cn – 1) + … + (b1 + c1) + (b0 + c0) = S(2an) + S(2an – 1) + … + S(2a0). Аналогично, 5M = 10n + 1kn + 10n(kn – 1 + pn) + … + + 10(k0 + p1) + p0, S(5M) = S(5an) + S(5an – 1) + … + S(5a0).
Очевидно, и S(2M), и S(5M) не зависит от порядка цифр ai в числе M,
поэтому S(2M) = S(2K), и S(5M) = S(5K).
Задача 3: Каково наибольшее возможное число вершин многоугольника, все стороны которого лежат на 6 прямых?
Решение:
Пример такого 12-угольника приведен на рис.13. Покажем, что требуемого многоугольника с большим числом вершин не существует. Предположим противное. Тогда, так как в многоугольнике число сторон равно числу вершин, найдется прямая, скажем l, содержащая не менее трех сторон многоугольника, а значит, не менее шести его вершин. Но остальные 5 прямых могут давать в пересечении с l не более пяти точек, поэтому на l лежит не более пяти вершин многоугольника – противоречие.
Задача 4: Существуют ли такие 100 треугольников, ни один из которых нельзя покрыть 99 остальными?
Решение:
Такие треугольники существуют. Мы построим даже бесконечное
семейство треугольников T1,T2,T3 … , ни один из которых
не покрывается остальными. Пусть все треугольники Ti равнобедренные
с основанием ai = 10i площади Si = (⅓)i. Построенное
семейство искомое. В самом деле, пусть некоторый треугольник семейства
(скажем, Tk) покрыт остальными. Проекция каждого треугольника
Tii ≤ k – 1 на прямую, содержащую сторону ak, не
превосходит наибольшей стороны Ti, т.е. не превосходит 10i,
а тогда сумма этих проекций не превосходит  . Тогда площадь Tk, покрытая треугольниками
T1,T2,T3 … ,Tk – 1 не превосходит
. Тогда площадь Tk, покрытая треугольниками
T1,T2,T3 … ,Tk – 1 не превосходит
 (здесь hk – высота
треугольника Tk), значит, оставшиеся
(здесь hk – высота
треугольника Tk), значит, оставшиеся  покрываются треугольниками Tk + 1,Tk + 2, … . Но это
невозможно, так как общая площадь всех этих треугольников равна
покрываются треугольниками Tk + 1,Tk + 2, … . Но это
невозможно, так как общая площадь всех этих треугольников равна
 – противоречие.
– противоречие.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVIII олимпиада, 1997-1998 >> Заочный тур >> 11 класс | Убрать решения |