 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVIII олимпиада, 1997-1998 >> Заочный тур >> 7 класс | Убрать решения |
|
|
| XXXVIII Екатеринбургская городская олимпиада, 1997-1998. Заочный тур. 7 класс |
|
|
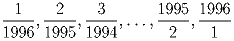
Решение:
Пусть найдутся такие дроби. Тогда
 , откуда
2nmk = 1997(nm + mk + kn) – 1997² = 1997(nm + mk + kn – 1997).
Так как 1997 – простое число, то 1997 делит либо n, либо m, либо k,
что невозможно, так как n < 1997, m < 1997, k < 1997.
, откуда
2nmk = 1997(nm + mk + kn) – 1997² = 1997(nm + mk + kn – 1997).
Так как 1997 – простое число, то 1997 делит либо n, либо m, либо k,
что невозможно, так как n < 1997, m < 1997, k < 1997.
Задача 2: Записав числа
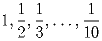
Решение:
Одно из решений:

З А М Е Ч А Н И Е:
Решения вида

не подходят, так как выражение  не определено.
не определено.
Задача 3: В треугольниках ∆ ABC и ∆ A′B′C′ стороны AB, BC, A′B′, B′C′ равны между собой. Треугольник ∆ A′B′C′ находится внутри ∆ ABC. Возможно ли такое?
Решение:
Да. Например:

Задача 4: Автомат при опускании гривенника выбрасывает пять«двушек", а при опускании «двушки" – пять гривенников. Может ли Петя, подойдя к автомату с одной «двушкой", получить после нескольких опусканий одинаковое количество «двушек" и гривенников?
Решение:
Заметим, что после любого обмена на руках у Пети остается нечетное число монет и, следовательно, у него никогда не будет одинакового количества «двушек" и гривенников.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVIII олимпиада, 1997-1998 >> Заочный тур >> 7 класс | Убрать решения |