 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVIII олимпиада, 1997-1998 >> Заочный тур >> 8 класс | Убрать решения |
|
|
| XXXVIII Екатеринбургская городская олимпиада, 1997-1998. Заочный тур. 8 класс |
|
|
Решение:
1 способ. Воспользуемся неравенством 2ab ≤ a² + b². Тогда 2a ≤ 1 + a², 2a² ≤ 1 + a4, 2a³ ≤ a² + a4. (1 + a + a²)² = 1 + a² + a4 + 2a + 2a² + 2a³ ≤ 1 + a² + a4 + (1 + + a²) + (1 + a4) + (a² + a4) = 3(1 + a² + a4).
2 способ. 3(1 + a² + a4) – (1 + a + a²)² = 2 + 2a² + 2a4 – 2a – 2a² – 2a³ = 2((1 – – a) – (1 – a)a³) = 2(a – 1)²(a² + a + 1) = 2(a – 1)²((a + ½)² + ¾)) ≥ 0.
3 способ. 3(1 + a² + a4) – (1 + a + a²)² = 2 + 2a² + 2a4 – 2a – 2a² – 2a³ = (1 – 2a + + a²) + (1 – 2a² + a4) + (a² – 2a³ + a4) = (1 – a)² + (1 – a²)² + (a – a²)² ≥ 0.
Задача 2: Пусть числа
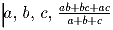 – целые.
Докажите, что число
– целые.
Докажите, что число 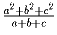 – целое.
– целое.Решение:
Доказательство следует из равенства.

Задача 3: Пусть
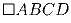 — квадрат. M — внутренняя точка квадрата.
Доказать, что точки пересечения медиан треугольников
∆ AMB, ∆ BMC, ∆ CMD, ∆ DMA
тоже образуют квадрат.
— квадрат. M — внутренняя точка квадрата.
Доказать, что точки пересечения медиан треугольников
∆ AMB, ∆ BMC, ∆ CMD, ∆ DMA
тоже образуют квадрат.Решение:
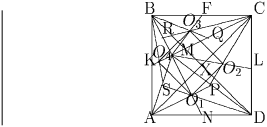
Обозначим точки пересечения медиан ∆ AMD, ∆ DMC, ∆ CMB, ∆ BMA через O1, O2, O3, O4, соответственно. И пусть MN, AP, DS, ML, DQ, CP, MF, CR, BQ, MK, AR, BS – медианы ∆ AMD, ∆ DMC, ∆ CMB, ∆ BMA, соответственно.
1 способ. Cм.рис.7.
Рассмотрим ∆ APC и ∆ O1PO2.
Они подобны по II признаку подобия треугольников (
∠ P — общий,  (точка пересечения медиан треугольника делит медиану в отношении
2:1, считая от вершины)).
Поэтому O1O2 = ⅓AC,
и ∠ O2O1P = ∠ CAP, откуда следует что
O1O2 || AC.
Аналогично рассматривая пары подобных треугольников
∆ ARC и ∆ O4RO3,
(точка пересечения медиан треугольника делит медиану в отношении
2:1, считая от вершины)).
Поэтому O1O2 = ⅓AC,
и ∠ O2O1P = ∠ CAP, откуда следует что
O1O2 || AC.
Аналогично рассматривая пары подобных треугольников
∆ ARC и ∆ O4RO3,
∆ BQD и ∆ O3QO2, ∆ BSD и ∆ O4SO1, доказываем, что O4O3 = ⅓AC, O4O3 || AC, O3O2 = ⅓BD, O3O2 || BD, O4O2 = ⅓BD, O4O1 || BD.
Диагонали квадрата 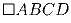 равны и взаимно перпендикулярны,
отсюда следует, что O1O2 = O2O3 = O3O4 = O4O1 и
равны и взаимно перпендикулярны,
отсюда следует, что O1O2 = O2O3 = O3O4 = O4O1 и  (
( как углы с взаимно
параллельными сторонами). Следовательно
как углы с взаимно
параллельными сторонами). Следовательно  — квадрат.
— квадрат.
2 способ. Cм. рис.8.
Легко доказывается, что  — квадрат (используя
∆ FBK = ∆ KAN = ∆ NDL = ∆ LCF).
Рассмотрим ∆ MFL и ∆ MO3O2.
Они подобны по II признаку подобия треугольников (
∠ M — общий,
— квадрат (используя
∆ FBK = ∆ KAN = ∆ NDL = ∆ LCF).
Рассмотрим ∆ MFL и ∆ MO3O2.
Они подобны по II признаку подобия треугольников (
∠ M — общий,  ).
Из подобия ∆ MFL ∽ ∆ MO3O2
следует равенство соответствующих углов и пропорциональность
соответствующих сторон. То есть O3O2 = ⅔FL и
∠ O3O2M = ∠ FLM, откуда следует что O3O2 || FL.
Аналогично рассматривая пары подобных треугольников
∆ MLN и ∆ MO2O1, ∆ MNK и ∆ MO1O4,
∆ MKF и ∆ MO4O3 доказываем, что
O1O2 = ⅔NL, O1O2 || NL,
O1O4 = ⅔KN, O1O4 || KN,
O4O3 = ⅔KF, O4O3 || KF.
).
Из подобия ∆ MFL ∽ ∆ MO3O2
следует равенство соответствующих углов и пропорциональность
соответствующих сторон. То есть O3O2 = ⅔FL и
∠ O3O2M = ∠ FLM, откуда следует что O3O2 || FL.
Аналогично рассматривая пары подобных треугольников
∆ MLN и ∆ MO2O1, ∆ MNK и ∆ MO1O4,
∆ MKF и ∆ MO4O3 доказываем, что
O1O2 = ⅔NL, O1O2 || NL,
O1O4 = ⅔KN, O1O4 || KN,
O4O3 = ⅔KF, O4O3 || KF.
А так как стороны квадрата  равны,
то O1O2 = O2O3 = O3O4 = O4O1.
равны,
то O1O2 = O2O3 = O3O4 = O4O1.  (
( как углы с взаимно
параллельными сторонами). Следовательно
как углы с взаимно
параллельными сторонами). Следовательно  — квадрат.
— квадрат.
3 способ. См. рис.9. Через точки O1, O2, O3, O4, проведем прямые A1D1 || AD, C1D1 || || CD, B1C1 || BC, A1B1 || AB, соответственно.
Докажем, что прямые A1D1 и A1B1 пересекаются в точке A1 ∈ AM. Пусть прямая A1D1 пересекает AM в точке A1. a прямая A1B1 пересекает AM в точке A′.
Рассмотрим ∆ AMN и ∆ A1MO1. Они подобны по трем углам ( ∠ M — общий, ∠ MA1O1 = ∠ MAN, ∠ MO1A1 = ∠ MNA, — как соответствующие углы при параллельных прямых AD и A1D1). Из подобия ∆ AMN ∽ ∆ A1MO1 следует пропорциональность соответствующих сторон. А так как MO1 = ⅔MN, то MA1 = ⅔MA. Аналогично, рассматривая пару подобных треугольников ∆ MKA и ∆ MO4A′, мы получим, что MA′ = ⅔MA, а следовательно, MA′ = MA1, то есть точки A′ и A1 совпадают. Аналогично доказывается, что прямые A1B1 и B1C1, B1C1 и C1D1 пересекаются в точках B1 ∈ BM, C1 ∈ CM, D1 ∈ DM, соответственно.
Из подобия ∆ AMN ∽ ∆ A1MO1 следует, что
A1O1 = ⅔AN = ⅓AD.
Аналогично рассматривая пару подобных треугольников
∆ MND и ∆ MO1D1 мы получим, что
O1D1 = ⅔ND = ⅓AD, то есть O1 — середина
отрезка A1D1.
Аналогично доказывается, что O2, O3, O4 — середины
отрезков C1D1, B1C1, A1B1, соответственно
и A1D1 = A1B1 = B1C1 = C1D1 = ⅔AD.
 как углы с взаимно
параллельными сторонами. Следовательно
как углы с взаимно
параллельными сторонами. Следовательно  — квадрат.
После чего легко доказывается, что
— квадрат.
После чего легко доказывается, что  — квадрат.
— квадрат.
4 способ.
Рассмотрим векторы:
 ,
,
 ,
,
 и
и
 .
.
Тогда
 .
.
Аналогично доказывается, что
 ,
,
 ,
,
 .
.
А так как диагонали квадрата  равны и взаимно перпендикулярны,
отсюда имеем, что стороны
равны и взаимно перпендикулярны,
отсюда имеем, что стороны  равны и взаимно перпендикулярны
и следовательно
равны и взаимно перпендикулярны
и следовательно  — квадрат.
— квадрат.
em:linewidth 0.4pt 0.60mm 0.4pt
Задача 4: Можно ли расставить в вершинах куба различные числа так, чтобы каждое число равнялось сумме трех, соединенных с ним ребрами куба?
Решение. Обозначим числа в в вершинах куба через a, b, c, d, f, k, l, m. Тогда
a = b + d + f
b = a + c + k
c = b + d + l
d = a + c + m
f = a + k + m
k = b + f + l
l = c + k + m
m = d + l + f
Сложив почленно эти равенства имеем: a + b + c + d + f + k + l + m = 3(a + b + c + d + f + k + l + m), откуда a + b + c + d + f + k + l + m = 0. Но a + b + c + d + f + k + l + m = a + (b + d + f) + l + (c + k + m) = 2a + 2l, откуда a = – l. Аналогично доказывается, что b = – m, c = – f, d = – k (*).
Отсюда получаем способ расстановки чисел: например, b = 1 d = 2 f = 3. Тогда по условию a = b + d + f = 6, а остальные числа находим из условия (*): l = – 6, c = – 3, m = – 1, k = – 2.
Ответ: можно.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVIII олимпиада, 1997-1998 >> Заочный тур >> 8 класс | Убрать решения |