Задача 1: Решить уравнение

где [A] – целая часть числа A, то есть наибольшее целое число, не превосходящее A.

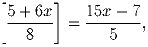
Решение:

Обозначим . Тогда , и уравнение после преобразований получает вид . Отсюда , и поэтому  – 1 < 30m ≤ 39. C учётом того, что m ∈ Z, получаем 2 решения: m = 0 и m = 1. Подставляя их в формулу , находим два решения задачи: и .

Ответ: , .

Задача 2: Число A вида 100 … 01 кратно 19.

Докажите, что A кратно 13.

Решение:

Заметим, что числа вида 10^l ± 1 (l = 1,\,2,\, … ,\,8) не делятся на 19, и 10⁹ + 1 = 19 • 52631579 – наименьшее целое число такого вида, делящееся на 19. Пусть n = 9k + l,(k ∈ N, l = 1,\,2,\, … ,\,8). Имеем

где M – натуральное число. Число A делится на 19 тогда и только тогда, когда l = 0, и k – нечётное число. То есть числа вида A = 10^9(2r + 1) + 1, (r = 0,\,1,\,2,\, … ) и только они (среди чисел вида 10^l + 1) делятся на 19. Из равенства (*) имеем: A = 10^9(2r + 1) + 1 = (10⁹ + 1) • M. Остаётся заметить, что число 10⁹ + 1 = 13 • 76923077 делится и на 13.

Задача 3: Треугольники  ∆ ABC и  ∆ OBC оба равносторонние. Точка M лежит на окружности с центром O и радиусом OB.

Докажите, что MB² + MC² = MA².

Решение:

Проведём дополнительное построение (см. рис.11.) Пусть TF = 2R — диаметр, и  ∠ TOM =  α . Из  ∆ MBO: , из  ∆ MCO: . По теореме косинусов из  ∆ MAO получим: . Для решения задачи остаётся проверить равенство MB² + MC² = MA², которое равносильно тождеству

Используя формулу , левую часть равенства приведём к виду , которая, очевидно, при любом  α  равна правой.

Задача 4: Все натуральные числа поделены на хорошие и плохие. Известно, что если n – хорошее, то и число n + 6 – хорошее, а если число m – плохое, то и число m + 15 – плохое.

Может ли среди первых 2000 чисел быть ровно 1000 хороших?

Решение:

Докажем методом от противного два утверждения:

1) если число k – хорошее, то число k + 3 также хорошее,

2) если число k – плохое, то число k + 3 также плохое.

В первом случае, пусть число k – хорошее, а число k + 3 – плохое. Тогда число k + 18 одновременно должно быть и хорошим, и плохим – противоречие.

Во втором случае если число k – плохое, а число k + 3 – хорошее, то число k + 15 одновременно является и хорошим, и плохим, чего быть не может.

Из доказанных утверждений следует, что в каждой тройке чисел вида 3k + 1, 3k + 2 и 3k + 3, (k = 0,\,1,\, … ) одно и то же количество хороших чисел, а значит среди первых 2000 чисел натурального ряда не может быть ровно 1000 хороших чисел.