 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXIX олимпиада, 1998-1999 >> Областной тур >> 10 класс >> 1-й день | Убрать решения |
|
|
| XXXIX Екатеринбургская городская олимпиада, 1998-1999. Областной тур. 10 класс. 1-й день |
|
|
Решение: Нет, это не верно. Пусть, от противного, найдётся натуральное M (можно полагать, M > 1) с таким свойством. Рассмотрим числа, лежащие в отрезке [M;M6] — их всего M6 – M + 1 штук. Каждое из таких чисел имеет вид a³ + b² для некоторых натуральных a и b. Ясно, что a ≤ M², b ≤ M³, поэтому всего различных пар (a;\,b) — M5. Имеем неравенство: M5 ≥ M6 – M + 1, что невозможно для M > 1. Противоречие. Задача 2: Первой точкой Брокара в треугольнике ABC называется такая точка P, что ∠ PAC = ∠ PCB = ∠ PBA. Из точки P опущены перпендикуляры
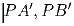 и
и 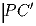 на стороны BC, CA и AB соответственно. Докажите, что
на стороны BC, CA и AB соответственно. Докажите, чтоа) треугольники ∆ ABC и 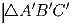 подобны;
подобны;
б) коэффициент их подобия равен 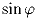 , где
, где 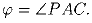
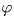 угол Брокара (
угол Брокара (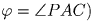 Рассмотрим четырёхугольник
Рассмотрим четырёхугольник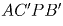 (см. рис.18).
У него два противоположных угла прямые, поэтому вокруг него
можно описать окружность. Но тогда
(см. рис.18).
У него два противоположных угла прямые, поэтому вокруг него
можно описать окружность. Но тогда 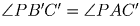 ,
как вписанные опирающиеся на одну и ту же дугу. Аналогично доказываются
равенства углов
,
как вписанные опирающиеся на одну и ту же дугу. Аналогично доказываются
равенства углов 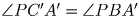 ,
,
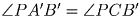 , и
, и 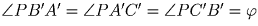 .
Отсюда следует во-первых, утверждение пункта а) задачи, а во-вторых,
что точка P также является и точкой Брокара треугольника
.
Отсюда следует во-первых, утверждение пункта а) задачи, а во-вторых,
что точка P также является и точкой Брокара треугольника
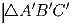 . Так как в подобных треугольниках
отношение любых соответствующих линейных элементов равно коэффициенту
подобия, то
. Так как в подобных треугольниках
отношение любых соответствующих линейных элементов равно коэффициенту
подобия, то 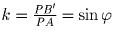 , что доказывает
пункт б).
, что доказывает
пункт б).
Задача 3: Числа a, b и c удовлетворяют равенствам: ab + bc + ac = 1999abc, и 1999(a + b + c) = 1. Найти a1999 + b1999 + c1999.
Решение: Из условия задачи следует, что
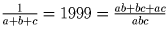 , откуда
a²b + a²c + b²a + b²c + c²a + c²b + 2abc = 0. Разложив на множители левую
часть, получим (a + b)(a + c)(b + c) = 0, откуда среди чисел a, b и c
есть два (без ограничения общности это a и b), дающих в сумме 0.
Тогда 1999c = 1, и
, откуда
a²b + a²c + b²a + b²c + c²a + c²b + 2abc = 0. Разложив на множители левую
часть, получим (a + b)(a + c)(b + c) = 0, откуда среди чисел a, b и c
есть два (без ограничения общности это a и b), дающих в сумме 0.
Тогда 1999c = 1, и 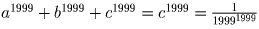 .
.ОТВЕТ: 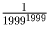 .
.
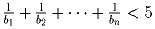 ?
?Решение: Верно. В самом деле, из условия следует, что все bi имеют вид
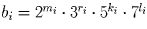 , причем
четвёрки (mi, ri, ki, li) различны при различных i.
Тогда
, причем
четвёрки (mi, ri, ki, li) различны при различных i.
Тогда 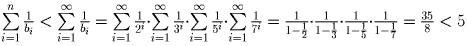 .
.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXIX олимпиада, 1998-1999 >> Областной тур >> 10 класс >> 1-й день | Убрать решения |