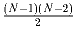Задача 1: В чемпионате школы по футболу участвуют N команд. Игры проводятся в один круг, за победу команде даётся 3 очка, за ничью — 1 очко, за поражение — 0 очков. Команда «Mатематики" торопилась на олимпиаду по математике, поэтому провела все свои матчи досрочно. После этого команда знала, что независимо от результатов оставшихся матчей, она займёт место не ниже k-го (1 ≤ k ≤ N). Какое наименьшее число очков могло быть у команды «Математики"?

Решение: Рассмотрим команды, занявшие по итогам турнира места с 1 по k + 1 (случай k = N опускаем ввиду его тривиальности). Они провели между собой 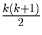матчей. Так как в каждой встрече «теряется" не менее, чем 3 очка, в играх между собой эти команды в сумме потеряли не менее 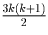очков; тогда по принципу Дирихле среди них есть команда, потерявшая не менее (а следовательно, набравшая не более 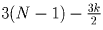) очков. Ясно, что это и есть команда, занявшая k + 1 место. Таким образом, набор «Математиками" 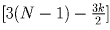+1 очка гарантирует им место не ниже k-го.

Покажем, что набор «Математиками" даже 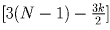очков может привести к тому, что «Математики" займут k + 1 место. Пусть «Математики" и ещё k команд теряют очки только во встречах между собой. Занумеруем эти команды в произвольном порядке числами от 1 до k + 1. Рассмотрим два случая:

1) k — чётно. Пусть команда с номером i, 1 ≤ i ≤ k + 1 проиграла матчи командам с номерами j той же чётности, 1 ≤ j < i, и командам с номерами j противоположной чётности, i < j ≤ k + 1, выигрыв у остальных. Тогда каждая из рассматриваемых команд набрала ровно 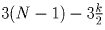очков, и любая из них (в том числе «Математики") может оказаться худшей, то есть занять место ниже k-го.

2) k — нечётно. Пусть матчи между командами 1 и 2, 3 и 4,  … , k и k + 1 завершились вничью, и каждая команда с номером i, 1 ≤ i ≤ k + 1 проиграла матчи командам с номерами j той же чётности, 1 ≤ j < i, и командам с номерами j противоположной чётности, i < j ≤ k + 1, (исключая случай i — нечётно, j = i + 1), выигрыв у остальных. Снова все эти команды набрали поровну очков, и вновь «Математики" могут оказаться среди них последними. Остаётся заметить, что число очков, набранное каждой из команд, равно .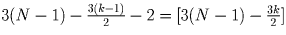

ОТВЕТ: 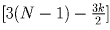очков при k < N, и 0 очков при k = N.

Задача 2: Про квадратные трехчлены f₁, f₂ и f₃ с разными старшими коэффициентами известно, что их разности f₁ – f₂, f₂ – f₃ и f₃ – f₁ имеют по одному корню. Докажите, что эти корни совпадают.

Решение: Обозначим f₁ = a₁x² + b₁x + c₁, f₂ = a₂x² + b₂x + c₂, f₃ = a₃x² + b₃x + c₃, a₁ – a₂ =  α  ≠ 0, a₂ – a₃ =  β  ≠ 0, a₃ – a₁ =  γ  ≠ 0. Но f₁ – f₂ = f₁ – f₃ + f₃ – f₂, то есть выполнено тождество  α (x – x₁)² ≡  –  γ (x – x₃)² –  β (x – x₂)², в котором  γ  =  –  α  –  β . Тогда

 α (x – x₁)² ≡ ( α  +  β )(x – x₃)² –  β (x – x₂)²(*).

Пусть, не ограничивая общности, a₁ < a₂ < a₃. Тогда  α ,\, β  < 0. Подставим в (*) x = x₃:  α (x₃ – x₁)² =  –  β (x₃ – x₂)². Поскольку  α  и  β  одного знака, то x₃ – x₁ = x₃ – x₂ = 0, откуда и следует утверждение задачи.

Задача 3: Пусть M — точка на диаметре AB окружности с центром в точке O; C и D — точки окружности, расположенные по одну сторону от AB и такие, что  ∠ CMA =  ∠ DMB,  ∠ OCM =  α . Чему равен угол  ∠ ODM?

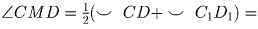
Решение: Продолжим CM и DM до пересечения с окружностью соответственно в точках D₁ и C₁ (см. рис.22). Из равенства  ∠ CMA =  ∠ DMB получаем, что точки C₁ и D₁ симметричны точкам C и D относительно диаметра AB. Тогда 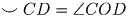. Из равенства  ∠ CMD =  ∠ COD получаем, что точки C, M, O, D лежат на одной окружности. Значит,  ∠ OCM =  ∠ ODM, так как они опираются на одну и ту же дугу этой окружности.

ОТВЕТ:  ∠ ODM =  α .

Задача 4: Каково наибольшее число подряд идущих членов последовательности x_n = n² + 1999, наибольший общий делитель которых больше 1?

Решение: Пусть d — общий делитель трёх подряд идущих членов последовательности — x_n, x_n + 1 и x_n + 2. Тогда число x_n + 2 – 2x_n + 1 + x_n = (n + 2)² – 2(n + 1)² + n² = 2 тоже делится на 2, то есть d = 1 или d = 2. Но d ≠ 2, так как среди любых двух подряд идущих членов последовательности один нечётен. Итак, d = 1, то есть не существует трёх подряд идущих членов последовательности, наибольший общий делитель которых больше 1.

Два таких числа существуют. Например, x₅ = 2024 и x₆ = 2035 делятся на 11.

ОТВЕТ: Два члена последовательности.