 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXIX олимпиада, 1998-1999 >> Областной тур >> 11 класс >> 2-й день | Убрать решения |
|
|
| XXXIX Екатеринбургская городская олимпиада, 1998-1999. Областной тур. 11 класс. 2-й день |
|
|
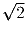 клетки каждый с
концами в узлах таблицы. Какое
наибольшее число таких отрезков,
попарно не имеющих общих точек, можно провести
в этом прямоугольнике?
клетки каждый с
концами в узлах таблицы. Какое
наибольшее число таких отрезков,
попарно не имеющих общих точек, можно провести
в этом прямоугольнике?Решение:
Из условия задачи следует, что каждый рассматриваемый отрезок — диагональ квадрата 1 × 1 клетка (назовём такой отрезок просто диагональю). Рассмотрим прямоугольник k × 2 клетки, k > 2 (см. рис. 23). Так как каждая диагональ проходит через один из узлов сетки, лежащий на отрезке AA1, то в рассматриваемом прямоугольнике нельзя провести более k + 1 попарно не пересекающихся диагоналей.
Теперь пусть во всём прямоугольнике проведено x попарно непересекающихся диагоналей, и пусть, для определённости, m ≥ n. Разделим весь прямоугольник 2n × 2m на n полос размера 2n × 2m каждая. В каждой полосе может проведено не более 2m + 1, поэтому x ≤ n(2m + 1) = m + (n – 1)m + n = mn + min m,\,n.
Построим пример, показывающий, как можно провести ровно m + (n – 1)m + n = mn + min m,\,n попарно непересекающихся диагоналей. См. рис.24 (по-прежнему, m ≥ n). В нижней полосе 1 × 2m, как и в каждой из (n – 1) следующих полос 2 × 2m проведено 2m диагоналей, а в самой верхней полосе 1 × 2m — ровно n штук. Всего m + (n – 1)m + n = mn + min m,\,n диагоналей. Пример построен.
ОТВЕТ: m + (n – 1)m + n = mn + min m,\,n диагоналей.
Задача 2:
Диагонали параллелограмма, отличного от прямоугольника, ABCD пересекаются в точке O. Докажите, что точка O, а также основания перпендикуляров, опущенных из точки A на прямые BC, BD и CD, лежат на одной окружности.
Решение: Пусть M, K и L — основания перпендикуляров, опущенных из вершины A на прямые DC, BC и DB соответственно. Возможны 4 случая:
а) точка L лежит вне параллелограмма (тогда угол ∠ BAD острый) — см. рис.25,
б) точка L лежит внутри параллелограмма, и угол ∠ BAD острый — см. рис.26,
в) угол ∠ BAD тупой, и обе точки M и K лежат на сторонах параллелограмма — см. рис.27,
г) угол ∠ BAD тупой, и одна из точек M и K (пусть K) лежит на стороне параллелограмма, а вторая — на продолжении стороны — см. рис.28.
Пусть ∠ KMO = α . Обозначим через β угол, дополнительный к углу ∠ KLO. Нам достаточно доказать, что α = β (тогда α + ∠ OLK = π , и вокруг четырёхугольника KLOM можно описать окружность). Построим на AC, как на диаметре, окружность. Тогда O — её центр, а точки M и K лежат на этой окружности. Отсюда OA = OM (то есть, треугольник OAM равнобедренный, и ∠ OAM = ∠ OMA), и ∠ KMA = ∠ KCA (как вписаные, опирающиеся на одну и ту же дугу). Кроме того, ∠ KCA = ∠ CAD. Имеем: α = ∠ KMO = ∠ AMO – ∠ AMK = ∠ OAM – ∠ CAD = ∠ DAM в случаях а)и б), α = ∠ KMO = ∠ AMK – ∠ AMO = ∠ CAD – ∠ OAM = ∠ DAM в случае в), α = ∠ KMA + ∠ OMA = ∠ CAD + ∠ OAM = ∠ DAM в случае г). Итак, ∠ DAM = α в любом случае.
Построим на AB, как на диаметре, окружность. Точки L и K лежат на этой окружности. Теперь в случае а) (так как четырёхугольник KLBA вписан в окружность) ∠ KAB = π – ∠ KLB = β . В остальных случаях ∠ KAB = ∠ KLB = β , так как углы ∠ KAB и ∠ KLB опираются на одну и ту же дугу. Остаётся заметить, что ∠ ABK = ∠ ADM, и ∆ ABK ∽ ∆ ADM по двум углам, откуда и следует равенство β = α .
Задача 3: Рассматривается система двух уравнений с двумя неизвестными:
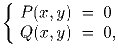 где P(x,y) и Q(x,y) —
многочлены по переменной x и по переменной y. Может ли эта
система иметь ровно три решения: (2;3), (0;2), (9;7)?
где P(x,y) и Q(x,y) —
многочлены по переменной x и по переменной y. Может ли эта
система иметь ровно три решения: (2;3), (0;2), (9;7)?Решение:
ОТВЕТ: Да, такое возможно. Приведём два из возможных решений.
1 способ: Пусть 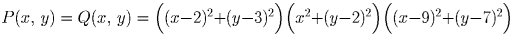 . Тогда система равносильна совокупности уравнений
. Тогда система равносильна совокупности уравнений
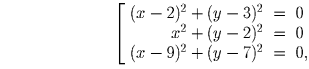
2 способ: Рассмотрим y1(x) = ax³ + bx² + cx + d и y2(x) = mx³ + nx² + + px + q — два многочлена третьей степени, графики которых проходят через точки (2,\,3), (0,\,2) и (9,\,7), и такие, что a ≠ m. Положим P(x,\,y) = y – (ax³ + bx² + cx + d) и Q(x,\,y) = y – (mx³ + nx² + px + q). Тогда система принимает вид:
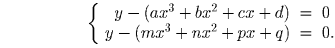
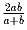 . Построить бесконечную последовательность
(или доказать, что такой не существует)
целых чисел, в которой каждый член, начиная со второго, равен
среднему гармоническому предшествующего и последующего членов
и в которой не все члены равны.
Решение:
. Построить бесконечную последовательность
(или доказать, что такой не существует)
целых чисел, в которой каждый член, начиная со второго, равен
среднему гармоническому предшествующего и последующего членов
и в которой не все члены равны.
Решение:
Таких последовательностей не существует. Рассуждаем от противного.
Заметим, что если 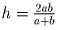 , то
, то 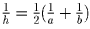 — среднее арифметическое чисел
— среднее арифметическое чисел 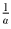 и
и 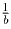 Докажем, что не существут такой бесконечной последовательности
чисел вида
Докажем, что не существут такой бесконечной последовательности
чисел вида 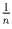 , n ∈ Z,
в которой не все члены равны, и каждый член, начиная со второго,
равен среднему арифметическому соседних с ним членов. По характеристическому
свойству арифметической прогрессии получаем, что наша последовательность
чисел вида
, n ∈ Z,
в которой не все члены равны, и каждый член, начиная со второго,
равен среднему арифметическому соседних с ним членов. По характеристическому
свойству арифметической прогрессии получаем, что наша последовательность
чисел вида 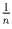 должна быть арифметической прогрессией (
должна быть арифметической прогрессией (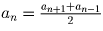 ,
следовательно, an + 1 – an = an – an – 1, и an —
арифметическая прогрессия). Замечаем, что все члены вида
,
следовательно, an + 1 – an = an – an – 1, и an —
арифметическая прогрессия). Замечаем, что все члены вида 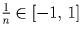 .
С другой стороны, |an|,
начиная с некоторого номера, должна неограничено возрастать.
Противоречие.
.
С другой стороны, |an|,
начиная с некоторого номера, должна неограничено возрастать.
Противоречие.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXIX олимпиада, 1998-1999 >> Областной тур >> 11 класс >> 2-й день | Убрать решения |