 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXIX олимпиада, 1998-1999 >> Областной тур >> 7 класс >> 2-й день | Убрать решения |
|
|
| XXXIX Екатеринбургская городская олимпиада, 1998-1999. Областной тур. 7 класс. 2-й день |
|
|
Решение: Незнайка не прав. В самом деле, пусть ему удалось отметить 15 точек, обладающих указанным свойством, и пусть li (1 ≤ i ≤ 7) — прямая, содержащая ровно i отмеченных Незнайкой точек. Так как все эти прямые различны, то любые 4 из них имеют не более 6 точек попарных пересечений, поэтому на прямых l7, l6, l5 и l4 лежит не менее 7 + 6 + 5 + 4 – 6 = 16 отмеченных точек — противоречие. Задача 2: На поле брани встретились армии Толстых и Тонких по 1000 человек в каждой. Сначала каждый Толстый выстрелил в одного из Тонких. Затем каждый уцелевший Тонкий выстрелил в одного из Толстых. Наконец, каждый уцелевший Толстый ещё раз выстрелил в одного из Тонких. После этого у каждой армии кончились патроны. Докажите, что в живых осталось не менее 500 солдат.
Решение: Пусть Тонкие своим единственным залпом убили n Толстых. Тогда вторым залпом Толстые убьют не более 1000 – n Тонких, поэтому за два последних залпа погибнет не более 1000 солдат с той и другой стороны.
Пусть после первого залпа Толстых в живых осталось x Тонких. Возможны два случая:
1) x ≤ 500. Тогда после залпа Тонких у Толстых останется в живых не менее 1000 – x солдат, что не меньше 500, и утверждение в этом случае доказано.
2) x > 500. Тогда после первого залпа Толстых у двух армий в сумме более 1500 живых солдат. Как показано выше, за два последних залпа не может погибнуть более 1000 человек, что и завершает доказательство.
Задача 3: Через точку плоскости проведены 3 прямые, разбивающие плоскость на 6 углов. Известно, что один из образовавшихся углов не превосходит полусуммы наибольшего и наименьшего угла. Докажите, что этот угол не превосходит 60.Решение: Обозначим три подряд идущих угла через α , β и γ . Оставшиеся три угла также будут соответственно равны α , β и γ , как вертикальные. Без ограничения общности, пусть α ≤ β ≤ γ . Тогда
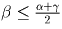 , откуда α + γ ≥ 2 β .
Но углы α , β и γ составляют развёрнутый угол, поэтому
π = α + β + γ ≥ 3 β , откуда и следует утверждение
задачи.
Задача 4:
Можно ли в вершинах и серединах сторон восьмиугольника расставить
натуральные числа от 1 до 16 так, чтобы сумма чисел на концах каждой
стороны равнялась числу в её середине.
, откуда α + γ ≥ 2 β .
Но углы α , β и γ составляют развёрнутый угол, поэтому
π = α + β + γ ≥ 3 β , откуда и следует утверждение
задачи.
Задача 4:
Можно ли в вершинах и серединах сторон восьмиугольника расставить
натуральные числа от 1 до 16 так, чтобы сумма чисел на концах каждой
стороны равнялась числу в её середине.Решение: Пусть удалось расставить числа так, как это требуется в задаче. Обозначим их через a1, a2, … , a16 двигаясь из какой-нибудь вершины восьмиугольника по часовой стрелке (см. рис.19). Тогда 2a2 = a1 + a3, 2a4 = a3 + a5, … , 2a16 = a15 + a1. Просуммируем 8 полученных равенств и добавим к обеим частям сумму a1 + a3 + … + a15. Получим 3(a1 + a3 + … + a15) = S, где S — сумма всех расставленных чисел. Значит, S делится на 3. Но S = 1 + 2 + … + 16 = 136 — противоречие.
ОТВЕТ: Расставить числа требуемым образом нельзя.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXIX олимпиада, 1998-1999 >> Областной тур >> 7 класс >> 2-й день | Убрать решения |