Задача 1: На доске в ряд выписаны n последовательных натуральных чисел. Двое играют в следующую игру: они по очереди разными мелками зачёркивают по одному из незачёркнутых ранее чисел, и так до тех пор, пока все числа не будут зачёркнуты. Если окажется, что первый игрок зачеркнул два рядом стоящих числа, то он проиграл, иначе — проиграл второй. Найдите все значения n, при которых первый игрок может выиграть независимо от игры второго игрока.

Решение: Непосредственной проверкой убеждаемся, что при n = 1, n = 2, или n = 4 первый игрок может добиться выигрыша, а при n = 3 — нет. Пусть n ≥ 5. Покажем, что второй игрок в этом случае имеет выигрышную стратегию. В самом деле, если начинающий своим первым ходом зачеркнул число k, не стоящее с краю, то второму достаточно зачёркивать любые числа, кроме k – 1 и k + 1 пока это возможно. Очевидно, что рано или поздно начинающему придётся зачеркнуть одно из этих чисел, и он проиграет. Пусть начинающий первым ходом зачеркнул 1 (или n, что одно и то же). Второй игрок зачёркивает n. Если второй ход первого игрока отличен от n – 1, то второй игрок побеждает, играя по схеме, указанной выше. Если второй ход первого игрока n – 1, то второй зачёркивает любые числа, кроме 2 и n – 2 (пока это возможно) и тоже гарантирует себе победу.

ОТВЕТ: 1, 2, 4.

Задача 2: В равнобедренном треугольнике ABC (AB = BC) на стороне AB взята точка K, а на стороне BC — точка L так, что AK = BL. Докажите, что KL не меньше половины AC.

Решение: Достроим треугольник ABC до параллелограмма ABDC и отметим на стороне CD точку M так, что CM = AK (см. рис.15). Треугольники  ∆ BKL и  ∆ CML равны (BL = CM, BK = CL,  ∠ KBL =  ∠ LCM), поэтому KL = ML. Четырёхугольник AKMC — параллелограмм (стороны AK и MC равны и параллельны), поэтому AC = KM. В силу неравенства треугольника KL + LM > KM, т.е. 2KL > AC, что и требуется.

Задача 3: Могут ли три человека, имея один двухместный велосипед, преодолеть расстояние 21 км за 3 часа? Скорость пешехода 5 км/ч, велосипедиста с пассажиром — 10 км/ч, а велосипедиста без пассажира – 15 км/ч.

Решение:

ОТВЕТ: Могут. Приведём два способа решения.

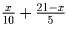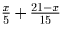1 способ: (с брошенным велосипедом). Двое проезжают на велосипеде xкм, оставляют его у дороги, а сами идут дальше пешком. Очевидно, при этом они на весь путь затратят часов, что не превосходит 3 при x ≥ 12. Третий идёт пешком первые xкм, а оставшийся путь едет на велосипеде; ему на дорогу требуется часов, что не более 3 при x ≤ 12. Значит, при x = 12км приведённый способ передвижения позволяет преодолеть дистанцию за 3 часа.

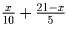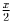2 способ:(с возвращающимся велосипедистом). Двое проезжают на велосипеде xкм, далее один из них идёт пешком (затрачивая на весь путь часов, что не превосходит 3 при x ≥ 12), а второй возвращается и забирает третьего (который всё это время шёл пешком). За время, затраченное первыми двумя на преодоление первых xкм, третий пройдёт км (его скорость ровно вдвое меньше), да ещё до встречи со вторым пройдёт 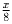км — всего 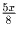км пешком, поэтому время, затраченное им на весь путь равно 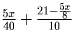часов, что не превосходит 3 при x ≤ 14,4км. Значит при любом x, удовлетворяющем условию 12 ≤ x ≤ 14,4 указанный способ передвижения решает задачу.

Задача 4: На доске были написаны числа от 1 до 9. Часть этих чисел стёрли и написали все произведения a × b из оставшихся на доске чисел (a ≠ b). Оказалось, что среди этих произведений нашлись числа, оканчивающиеся на все цифры от 0 до 9. Какое наибольшее количество чисел могло быть стёрто с доски?

Решение: На доске должно остаться число 5. Цифры 1 и 9 могли быть получены только в произведениях 3 • 7 и 1 • 9, значит, все нечётные числа были оставлены. Ещё необходимо одно чётное число, значит, на доске было оставлено не менее шести чисел. Легко убедиться в том, что попарные произведения шести чисел 1, 2, 3, 5, 7, 9 оканчиваются на все цифры от 0 до 9.

ОТВЕТ: 6 чисел.