Задача 1: Король приказал чеканить монеты. Порядок выпуска монет был определен так. Сначала чеканятся монеты в наименьшую возможную сумму — 1 крона. Затем на каждом следующем шаге казначей определяет наименьшую целочисленную сумму, которую нельзя набрать десятью или меньшим числом уже отчеканенных монет, и выпускаются монеты достоинством в эту сумму. Какие монеты будут выпущены в королевстве?

Решение:

ОТВЕТ: Монеты в 1, 11, 21, 31, 41, …крон.

В самом деле, если взять 2,3,4, … ,10 таких монет, то получится сумма, оканчивающаяся на цифру 2,3,4, … ,0 соответственно, то есть большую монету меньшими так разменять невозможно. С другой стороны, любую сумму S можно набрать не более чем 10-ю монетами, взяв самую большую монету, не превосходящую S и добавив не более 9 однокроновых монет.

Задача 2: Решите систему уравнений в натуральных числах n и m:

Здесь через S(k) обозначается сумма цифр натурального числа k.

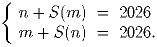
Решение: Имеем 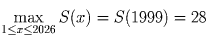. Значит, 1 ≤ S(x), S(y) ≤ 28. Отсюда 1998 ≤ x,y ≤ 2025. Выделим два очевидных решения (1998; 1999) и (1999; 1998). Пусть теперь x, y ≥ 2000. Тогда 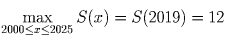, откуда 1 ≤ S(x), S(y) ≤ 12, и 2014 ≤ x, y ≤ 2025 (x, y ∈ N). Перебором приходим ещё к девяти решениям: (2014; 2019), (2015; 2018), (2016; 2017), (2017; 2016), (2018; 2015), (2019; 2014), (2020; 2022), (2021; 2021), (2022; 2020).

ОТВЕТ: 11 решений.

Задача 3: Бумажный треугольник ABC перегнули по прямой, в результате чего вершина C попала на сторону AB, а непокрытая часть разбилась на два равнобедренных треугольника, у которых равные стороны сходятся в вершинах A и B. Найдите угол C.

Решение: Обозначим три подряд идущих угла через  α ,  β  и  γ . Оставшиеся три угла также будут соответственно равны  α ,  β  и  γ , как вертикальные. Без ограничения общности, пусть  α  ≤  β  ≤  γ . Тогда 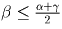, откуда  α  +  γ  ≥ 2 β . Но углы  α , β  и  γ  составляют развёрнутый угол, поэтому  π  =  α  +  β  +  γ  ≥ 

 ≥ 3 β , откуда и следует утверждение задачи.

Задача 4: Барон Мюнгхаузен утверждает, что он придумал такое натуральное число, что для любых натуральных чисел n и k, не больших 1999, это число можно представить в виде произведения n различных натуральных чисел, являющихся точными k-ми степенями. Может ли утверждение барона быть истинным?

Решение: Барон, как всегда, совершенно прав. Пусть p₁,\,p₂,\, … ,\,p_M — различные простые числа (M — любое число, делящееся на все числа от 1 до 1999, например, 1999!). Тогда число A = (p₁ • p₂ •  …  • p_M)^M — искомое. В самом деле, пусть n и k — любые числа, не превосходящие 1999. Тогда M = n • a = k • b, a,\,b ∈ N, и A = ((p₁ • p₂ •  … \,p_a)^b)^k • ((p_a + 1 • p_a + 2 •  … \,p_2a)^b)^k • ((p_{(n – 1)a + 1} • p_{(n – 1)a + 2} •  … \,p_na)^b)^k.