 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXIX олимпиада, 1998-1999 >> Областной тур >> 9 класс >> 1-й день | Убрать решения |
|
|
| XXXIX Екатеринбургская городская олимпиада, 1998-1999. Областной тур. 9 класс. 1-й день |
|
|
 .
.Решение: Разобъём прямоугольник на 7 фигур так, как показано на рис.16. Согласно принципу Дирихле по крайней мере в одну из фигур попадут 2 точки. Остаётся заметить, что диаметр каждой фигуры ровно
 .
.Задача 2: Первой точкой Брокара в треугольнике ABC называется такая точка P, что ∠ PAC = ∠ PCB = ∠ PBA. Пусть прямые AP, BP и CP пересекают описанную окружность треугольника ABC в точках A1, B1 и C1. Докажите, что ∆ ABC = ∆ A1B1C1.
Решение: Углы ∠ A1AC, ∠ B1BA и ∠ C1CB равны, и вписаны в одну и ту же окружность (см.рис.17), поэтому равны и дуги, на которые они опираются. Но тогда треугольник ∆ A1B1C1 получается из треугольника ABC поворотом вокруг центра описанной окружности на угол 2 ∠ CAA1.
Задача 3: Пусть действительные числа x, y и z удовлетворяют неравенству
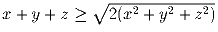 . Докажите, что тогда
|x| + |y| + |z| = x + y + z.
. Докажите, что тогда
|x| + |y| + |z| = x + y + z.Решение: Докажем эквивалентное утверждению: среди чисел x, y и z нет отрицательных. Очевидно, все три числа отрицательными быть не могут. Пусть отрицательное число ровно одно (без ограничения общности это z). Тогда
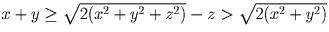 , что после
возведения в квадрат даёт невозможное неравенство 2xy > x² + y²,
поэтому этот случай невозможен.
Аналогично доказывается невозможность случая, когда среди чисел
x, y и z ровно 2 отрицательных. Остаётся единственный вариант
x ≥ 0, y ≥ 0, z ≥ 0. Утверждение доказано.
Задача 4:
Верно ли, что число 1999²ººº – 1 делится
, что после
возведения в квадрат даёт невозможное неравенство 2xy > x² + y²,
поэтому этот случай невозможен.
Аналогично доказывается невозможность случая, когда среди чисел
x, y и z ровно 2 отрицательных. Остаётся единственный вариант
x ≥ 0, y ≥ 0, z ≥ 0. Утверждение доказано.
Задача 4:
Верно ли, что число 1999²ººº – 1 делитсяa) на 1 000 000?
б) на 10 000 000?
Решение: Обозначим 1999² = 3996001 через t. Тогда 1999²ººº – 1 = t¹ººº – 1 = (t – 1)(t1999 + t1998 + … + t² + t + 1). Первая скобка, очевидно, делится на 1000, но не делится на 10 000. Вторая скобка является суммой 1000 слагаемых, каждое из которых имеет вид n • 1000 + 1, где n — чётное число, поэтому эта скобка также делится на 1000, но не на 10 000. Таким образом, число 1999²ººº – 1 делится на 1 000 000 и не делится на 10 000 000.
ОТВЕТ: а) делится; б) не делится.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXIX олимпиада, 1998-1999 >> Областной тур >> 9 класс >> 1-й день | Убрать решения |