Задача 1: Пусть a, b и c — целые неотрицательные числа такие, что 28a + 30b + 31c = 365. Найдите все значения, которые может принимать сумма a + b + c.

Решение: Покажем, что сумма a + b + c может равняться 12. Вот одно из решений: a = 1 (февраль), b = 4 (апрель, июнь, сентябрь, ноябрь) c = 7 (все остальные месяцы в году). Ещё решение: a = 2, b = 1, c = 9.

Покажем, что 12 — единственно возможное значение a + b + c. Пусть a + b + c ≤ 11. Тогда 28a + 30b + 31c ≤ 11 • 31 = 341 — противоречие. Пусть a + b + c ≥ 13. Тогда 28a + 30b + 31c ≥ 13 • 28 = 364, причём равенство достигается только при a = 13, b = c = 0. Во всех остальных случаях 28a + 30b + 31c ≥ 366. Противоречие.

Ответ: 12

Задача 2: В каждую клетку таблицы (2n + 1) × (2n + 1) записано число +1 или -1. Пусть p_i — произведение чисел i-ой строки, q_j — произведение чисел j-го столбца. Докажите, что .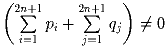

Решение:

В таблице из одних единиц 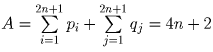. Замена одной единицы на число  – 1 приводит к тому, что суммы 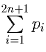и 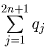либо обе уменьшаются на 2, либо обе увеличиваются на два, либо одна на два уменьшается, а другая на 2 увеличивается. Во всех случаях число A либо не изменяется, либо меняется на  ± 4. Из таблицы единиц за конечное число таких замен получаем любую таблицу из единиц и минус единиц. При этом число A будет отличаться от числа 4n + 2 на число, кратное 4, и поэтому не может стать равным нулю.

Задача 3: Из квадрата 5 × 5 вырезали центральную клетку. Как разрезать получившуюся плоскую фигуру на 2 части, которыми целиком можно обклеить куб 2 × 2 × 2?

Решение: см. рисунки 5a — 5c:

Задача 4: Числа x, y и z удовлетворяют равенству x + y + z – 2(xy + yz + zx) = ½ – 4xyz. Докажите, что хотя бы одно из них равно ½.

Решение:

Утверждение немедленно следует из равенства: x + y + z – 2(xy + yz + xz) + 4xyz – ½ = ½(2x – 1)(2y – 1)(2z – 1).