 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXIX олимпиада, 1998-1999 >> Районный тур >> 11 класс | Убрать решения |
|
|
| XXXIX Екатеринбургская городская олимпиада, 1998-1999. Районный тур. 11 класс |
|
|
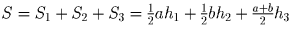 . Если и a, и b меньше ½, то эта величина
меньше, чем ¼h1 + ¼h2 + ½h3 = ¼(h1 + h2 + h3) + ¼h2 < ½, так как сумма высот
не превосходит стороны квадрата. Противоречие.
Задача 2:
Дорога протяжённостью 1км полностью освещена фонарями, причём
каждый фонарь освещает отрезок длиной 10м. Какое наибольшее количество
фонарей может быть на дороге, если известно, что после выключения
любого фонаря дорога будет освещена уже не полностью?
. Если и a, и b меньше ½, то эта величина
меньше, чем ¼h1 + ¼h2 + ½h3 = ¼(h1 + h2 + h3) + ¼h2 < ½, так как сумма высот
не превосходит стороны квадрата. Противоречие.
Задача 2:
Дорога протяжённостью 1км полностью освещена фонарями, причём
каждый фонарь освещает отрезок длиной 10м. Какое наибольшее количество
фонарей может быть на дороге, если известно, что после выключения
любого фонаря дорога будет освещена уже не полностью?Решение:
Ответ: 198. Занумеруем фонари натуральными числами в порядке следования вдоль дороги. Если отрезки, освещённые n-ым и n + 2-ым фонарями пересекаются, то n + 1-ый фонарь можно выключить. Следовательно, отрезки с различными нечётными номерами не пересекаются. На отрезке длины 1000м нельзя расположить больше 99 непересекающихся отрезков длины 10м, значит, фонарей не больше 198.
Расположим 198 фонарей так, чтобы центры освещенных отрезков образовывали арифметическую прогрессию, первый член которой равен 5м, а 98-ой — 995м. Между n-ым и n + 2-ым фонарём остаётся зазор, который освещается только n + 1-ым фонарём. Поэтому никакой фонарь выключить нельзя.
Задача 3: Про непрерывную функцию f известно, что:а) f определена на всей числовой прямой;
б) f в каждой точке имеет производную (и, таким образом, график f в каждой точке имеет единственную касательную);
в) график функции f не содержит точек, одна координата которых рациональна, а вторая — иррациональна.
Следует ли отсюда, что график f — прямая?
Решение:
Нет, не следует. Пример:
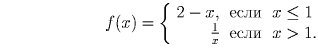
Решение:
Пусть 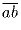 — двузначное число, обладающее требуемым
свойством. Тогда числа
— двузначное число, обладающее требуемым
свойством. Тогда числа 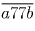 и
и 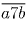 , а
следовательно, и их разность, равная 100(9a + 7) делятся на 13. Так
как 100 и 13 взаимно просты, на 13 делится число 9a + 7, откуда
перебором всех возможных случаев получаем, что a может равняться только 5.
Из делимости на 13 числа
, а
следовательно, и их разность, равная 100(9a + 7) делятся на 13. Так
как 100 и 13 взаимно просты, на 13 делится число 9a + 7, откуда
перебором всех возможных случаев получаем, что a может равняться только 5.
Из делимости на 13 числа 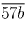 находим, что b = 2,
то есть 52 — единственно возможный
вариант.
находим, что b = 2,
то есть 52 — единственно возможный
вариант.
Убеждаемся, что все числа вида  делятся на 13. Это
немедленно следует из
равенства:
делятся на 13. Это
немедленно следует из
равенства: 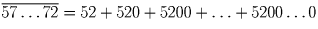 .
.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXIX олимпиада, 1998-1999 >> Районный тур >> 11 класс | Убрать решения |