 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXIX олимпиада, 1998-1999 >> Районный тур >> 8 класс | Убрать решения |
|
|
| XXXIX Екатеринбургская городская олимпиада, 1998-1999. Районный тур. 8 класс |
|
|
а) на 0.01;
б) на 0.005?
Решение:
а) Да, например:
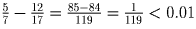 .
.
б) Нет. 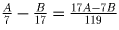 . 17A – 7B — целое число,
неравное нулю. Поэтому
. 17A – 7B — целое число,
неравное нулю. Поэтому 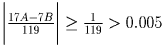 .
.
Задача 2: В республике прошли выборы в парламент. Все голосовавшие за партию «Лимон" любят лимоны, а среди избирателей, голосовавших за другие партии, 90 процентов лимоны не любят. Сколько процентов голосов набрала партия «Лимон", если ровно 46 процентов участвовавших в голосовании любят лимоны?
Решение:
Пусть M человек голосовали за "Лимон", а N — за другие
партии. Тогда M + 0,1N голосовавших любят лимоны, а всего
голосовавших M + N, поэтому
M + 0,1N = 0,46(M + N). Из полученного уравнения находим 3M = 2N, откуда
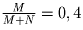 .
.
Ответ: 40 процентов.
Задача 3: Все 8 вершин замкнутой пространственной несамопересекающейся восьмизвенной ломаной совпадают с вершинами куба. Докажите, что у этой ломаной найдутся четыре звена одинаковой длины.
Решение: Все звенья ломаной — это либо рёбра куба (назовём их звеньями 1-го типа), либо диагонали его граней (звенья 2-го типа), либо диагонали куба (звенья третьего типа). Так как любые две диагонали куба пересекаются, в ломаной нет двух звеньев третьего типа, значит звеньев первого и второго типов в сумме не менее семи. По принципу Дирихле звеньев какого-то типа не менее четырёх. Остаётся заметить, что звенья каждого типа равны между собой по длине. Задача 4: Деду Морозу сшили новый мешок для новогодних подарков. Этот мешок был точно рассчитан на 12 тигрят и 15 слонят, или на 30 слонят и на 10 мартышек, или на 45 мартышек и 13 тигрят. А на сколько одних только тигрят рассчитан новый мешок Деда Мороза?
Решение: Пусть вместимость мешка Деда Мороза — A. Тогда имеем систему:
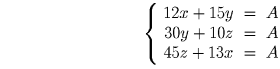
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXIX олимпиада, 1998-1999 >> Районный тур >> 8 класс | Убрать решения |