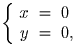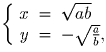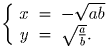Задача 1:
Решите систему уравнений относительно x и y:
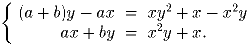
(a и b — заданные отрицательные числа).
Решение: Система линейная относительно a и b. Выразим эти неизвестные через
x и y. Вычтем из первого уравнения второе: a(y – 2x) = xy(y – 2x).
Случай y = 2x приводит к решению (0;0). В случае a = xy получаем 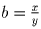 .
Отсюда с учетом того, что числа a и b отрицательные, получаем еще 2
решения.
.
Отсюда с учетом того, что числа a и b отрицательные, получаем еще 2
решения.
Ответ:
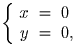
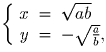
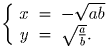
Задача 2:
Дедушка, бабушка, папа и мама подошли ночью к мосту (с одной стороны)
и хотят перейти через него. У них есть на всех один фонарик, без которого
невозможно и шага ступить. Мост выдерживает только двух человек. Папа
может перейти мост за 1 минуту, мама — за 2 минуты, дедушка — за
5 минут, бабушка — за 10 минут. Как им всем перейти мост за 17
минут?
Решение:
Сначала переходят мост мама и папа (2 минуты), затем мама
возвращается (2 минуты) и передает фонарик дедушке с бабушкой,
которые переходят мост (10 минут). Наконец, папа возвращается (1
минута) и вместе с мамой переходит мост (2 минуты).
Задача 3:
Выпуклый пятиугольник вписан в окружность. Известно, что все его
диагонали равны между собой. Докажите, что все его внутренние углы
равны между собой, и что все его стороны также равны между собой.
Решение:
Пусть ABCDE — пятиугольник, о котором идёт речь в задаче.
Так как EB = AC (см. рис.4), имеем равенство дуг
AB + BC = AC = EB = EA + AB, откуда дуги BC и EA равны.
Аналогично доказываются равенства EA = CD, CD = AB, и AB = DE.
Таким образом,
вершины
пятиугольника разбивают окружность на равные части, то есть пятиугольник
правильный.
Задача 4:
Является ли число 4
9 + 6¹º + 3²º простым?
Решение:
Не является. 4
9 + 6¹º + 3²º = (2
9)² + 2 • 2
9 • 3¹º + (3¹º)² = (2
9 + 3¹º)².


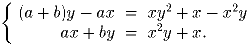
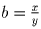 .
Отсюда с учетом того, что числа a и b отрицательные, получаем еще 2
решения.
.
Отсюда с учетом того, что числа a и b отрицательные, получаем еще 2
решения.