Задача 1:
Решите уравнение: 2x = 3[x] + 4,
где [x] — целая часть числа
x, то есть наибольшее целое число, не превосходящее x.
Решение:
Из условия следует, что число 2x — целое. Поэтому x либо целое,
либо является дробью со знаменателем 2. В первом случае [x] = x,
откуда x = – 4, а во втором —
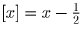
, откуда x = – 2,5.
Ответ: x = – 4, x = – 2,5.
Задача 2:
Семиклассник разрезал бумажный квадрат на прямоугольники периметра
7см, а восьмиклассник — такой же квадрат на прямоугольники периметра
8см. Может ли у восьмиклассника оказаться больше прямоугольников?
Решение:
Да, такое возможно. Например, пусть длина стороны разрезаемого
квадрата равна 42 см, семиклассник разрезает его на 21 • 28 = 588 прямоугольников размера 2 × 1,5 см, а
восьмиклассник — на 12 • 84 = 908 прямоугольников размера
3,5 × 0,5 см (возможность таких разрезаний очевидна).
Задача 3:
100 спортсменов, одетые в красные или синие костюмы построились
в одну шеренгу. Оказалось, что если спортсмен в красном костюме, то
спортсмен, стоящий от него через 9 человек, обязательно в синем.
Какое наибольшее количество спортсменов может быть одето в красные
костюмы?
Решение:
Занумеруем спортсменов натуральными числами от 1 до 100 в
порядке их располдожения в шеренге. Разобьем спортсменов на пары по
номерам: 1 и 11, 2 и 12, 3 и 13, … , 10 и 20, 21 и 31, 22 и
32, … , 89 и 99, 90 и 100. По условию в каждой из пар хотя бы
один спортсмен не одет в красный костюм. Таким образом, в красные
костюмы не может быть одето более 50 спортсменов.
Может случится, что 50 спортсменов в красных костюмах найдутся.
Например, в красное одеты все спортсмены с номерами с 1 по 10, с 21 по
30, с 41 по 50, с 61 по 70 и с 81 по 90. Таким образом 50 — искомое
число.
Задача 4:
Найдите все натуральные числа n, такие, что числа n + 19 и n + 98
одновременно
являются квадратами целых чисел.
Решение:
Пусть n + 98 = a², n + 19 = b², где a и b — целые числа
(очевидно, их можно считать неотрицательными). Тогда
(a + b)(a – b) = a² – b² = = 79 — число простое. Отсюда a + b = 79, a – b = 1, следовательно a = 40, b = 39, n = 1502.
Ответ: 1502.


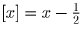 , откуда x = – 2,5.
, откуда x = – 2,5.