 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXIX олимпиада, 1998-1999 >> Заочный тур >> 8 класс | Убрать решения |
|
|
| XXXIX Екатеринбургская городская олимпиада, 1998-1999. Заочный тур. 8 класс |
|
|
 и
и 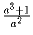 не меньше двух.
Решение:
не меньше двух.
Решение:
Первый способ. Пусть, от противного,
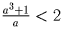 и
и 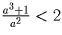 . Перемножим неравенства почленно
(это допустимо, так как все числа положительны) и заменим a³ на t.
Получим неравенство
. Перемножим неравенства почленно
(это допустимо, так как все числа положительны) и заменим a³ на t.
Получим неравенство 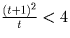 , где t > 0. Последнее
неравенство легко приводится к виду (t – 1)² < 0, которое не выполняется
ни для каких t.
, где t > 0. Последнее
неравенство легко приводится к виду (t – 1)² < 0, которое не выполняется
ни для каких t.
Второй способ. Снова предположим, что
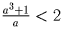 и
и 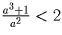 . Сложим неравенства почленно
и преобразуем получившееся неравенство:
. Сложим неравенства почленно
и преобразуем получившееся неравенство:
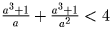
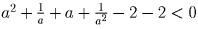
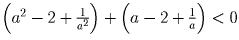
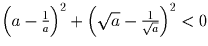 —
противоречие.
—
противоречие.
Решение:
Ответ: две диагонали. Покажем сначала, что трёх хороших диагоналей не может быть. Предположим противное. Тогда так как каждая диагональ соединяет две вершины из пяти, у пятиугольника (обозначим его ABCDE) найдётся вершина (скажем, A), из которой выходят две хорошие диагонали AC и AD. Но тогда площадь каждого из треугольников ABC и ADE равна половине площади пятиугольника, то есть площадь треугольника ACD равна нулю. Противоречие.
Построим пятиугольник с двумя хорошими диагоналями. Рассмотрим
равнобедренную трапецию ABDE, диагонали которой перпендекулярны и
делятся точкой пересечения O в отношении 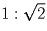 — см. рис. 7.
Построим точку C таким образом, чтобы четырёхугольник OBCD оказался
квадратом. Тогда площади треугольников AOB и DOE равны (так как
эти треугольники образованы диагоналями трапеции и примыкают к её боковым
сторонам), площадь треугольника AOE вдвое больше площади
треугольника BOD (так как эти треугольники подобны с коэффициентом
— см. рис. 7.
Построим точку C таким образом, чтобы четырёхугольник OBCD оказался
квадратом. Тогда площади треугольников AOB и DOE равны (так как
эти треугольники образованы диагоналями трапеции и примыкают к её боковым
сторонам), площадь треугольника AOE вдвое больше площади
треугольника BOD (так как эти треугольники подобны с коэффициентом
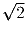 ) и равна площади квадрата OBCD, а значит, диагонали
AD и BE пятиугольника ABCDE — хорошие.
) и равна площади квадрата OBCD, а значит, диагонали
AD и BE пятиугольника ABCDE — хорошие.
Задача 3: Пончик закусывал в придорожном кафе, когда мимо него прошёл автобус. Через 3 плюшки мимо Пончика проехал мотоцикл, а ещё через 3 — автомобиль. Мимо Сиропчика, который закусывал в другом кафе у того же шоссе, они проехали в таком порядке: автобус, через 3 плюшки — автомобиль и ещё через 3 — мотоцикл. Скорость автомобиля равна 60 км/ч, мотоцикла — 30 км/ч. Чему равна скорость автобуса, если Пончик и Сиропчик поглощают плюшки с одной и той же одинаковой скоростью?
Решение: Пусть t(ч) — время, за которое Пончик съедает три плюшки, x(км/ч) — скорость автобуса. В момент времени, когда мимо Пончика проехал автомобиль, автобус находился от него на расстоянии 2xt км, а мотоцикл — на расстоянии 30t км. Cпустя a часов, в тот момент времени, когда мимо Сиропчика проехал мотоцикл, автомобиль находился от него на расстоянии 60t км, а автобус — на расстоянии 2xt км от мотоцикла, следовательно, на расстоянии 2xt – 60t км от автомобиля. Сравнивая расстояния, пройденные автомобилем и мотоциклом получаем уравнение a(60 – 30) = 60t + 30t, откуда
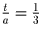 , а
сравнивая расстояния, пройденные автобусом и автомобилем, получаем
уравнение a(60 – x) = (2xt – (2xt – 60t)) = 60t, откуда
, а
сравнивая расстояния, пройденные автобусом и автомобилем, получаем
уравнение a(60 – x) = (2xt – (2xt – 60t)) = 60t, откуда  .
.Ответ: 40 км/ч.
Задача 4: Можно ли так вписать в таблицу 8 × 8 числа от 1 до 64 (каждое число ровно 1 раз), так чтобы сумма любых двух чисел, стоящих в клетках, имеющих общую сторону или вершину, не делилась бы на 4?Решение: Заметим, что среди чисел от 1 до 64 ровно 16 при делении на четыре дают остаток 1, ровно 16 — 2, ровно 16 — 3, и ровно 16 делятся без остатка (т.е. остаток равен нулю). Очевидно, сумма двух целых чисел делится на четыре тогда и только тогда, когда делится на четыре сумма их остатков. Задачу, следовательно, можно переформулировать следующим образом: можно ли в таблицу 8 × 8 вписать нули, единицы, двойки и тройки по 16 экземпляров каждого числа так, чтобы ни в каких клетках, имеющих общую сторону или вершину не стояли ни два нуля, ни две двойки, ни единица с тройкой. Рис.8 показывает, что такое размещение возможно.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXIX олимпиада, 1998-1999 >> Заочный тур >> 8 класс | Убрать решения |