 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXIX олимпиада, 1998-1999 >> Заочный тур >> 9 класс | Убрать решения |
|
|
| XXXIX Екатеринбургская городская олимпиада, 1998-1999. Заочный тур. 9 класс |
|
|
Решение: Обозначим через S сумму a + b + c + d. Тогда (a + b + c + d + 1)² = (S + 1)² = (S – 1)² + 4S ≥ 4S. C другой стороны a ≥ a² (так как 0 ≤ a ≤ 1), и это же верно для чисел b,\,c и d. Таким образом, имеем 4S ≥ 4(a² + b² + c² + d²), что завершает доказательство. Задача 2: На продолжении стороны AC треугольника ABC за точку A отмечена точка D. С помощью циркуля и линейки постройте на стороне BC точку E такую, что площади треугольников DEC и ABC равны.
Решение:
Исследование. Пусть задача решена, и такая точка построена. Обозначим через K точку пересечения отрезков DE и AB (см.рис.9). Из равенства SADK + SAKEC = SDEC = SABC = SAKEC + SBKE, следует равенство площадей треугольников ADK и BKE, а следовательно, и равенство SDAB = SDEB. Это означает, что точки A и E равноудалены от прямой BD, т.е, что четырёхугольник ADBE — трапеция.
Построение. Проводим через точку A прямую, параллельную прямой BD, и на пересечении этой прямой со стороной BC отмечаем точку E. Точка E искомая.
Доказательство. Четырёхугольник ADBE является трапецией по построению, следовательно площади треугольников DKA и BKE равны. Тогда равновелики и треугольники DEC и BAC.
Анализ. Из исследования видно, что задача всегда имеет единственное решение.
Задача 3: В треугольнике площади 2 расположены 15 точек, никакие три из которых не лежат на одной прямой. Докажите, что существует треугольник с вершинами в этих точках, площадь которого меньше, чем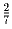 .
.Решение: Разделим одну из сторон данного треугольника (скажем, AB) на 7 равных частей и соединим точки деления с вершиной C (см. рис.10). Треугольник ABC разобъётся на 7 треугольников площади
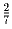 каждый. По принципу
Дирихле в некоторый такой треугольник (скажем, в заштрихованный)
попадут по крайней мере 3 точки.
Если не все из них совпадают с вершинами заштрихованного треугольника,
то площадь
треугольника с вершинами в этих точках строго меньше
каждый. По принципу
Дирихле в некоторый такой треугольник (скажем, в заштрихованный)
попадут по крайней мере 3 точки.
Если не все из них совпадают с вершинами заштрихованного треугольника,
то площадь
треугольника с вершинами в этих точках строго меньше
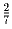 , и всё доказано. Пусть все эти точки совпадают с вершинами
треугольника и других точек в этом треугольнике нет. Тогда в оставшихся
шести треугольников разбиения лежат ещё 12 точек,
т.е. либо в некотором треугольнике лежат
по крайней мере 3 точки, не совпадающих с C (и тогда они искомые), либо
в каждом из оставшихся треугольников лежат ровно 2 точки.
Тогда выберем 2 точки в треугольнике соседнем к заштрихованному и добавим
точку C. Эти три точки, очевидно, искомые.
Задача 4:
Назовём трёхзначное число особенным, если из него можно вычеркнуть
цифру так, что образовавшееся число будет меньше суммы цифр
исходного трёхзначного. Сколько существует особенных чисел?
, и всё доказано. Пусть все эти точки совпадают с вершинами
треугольника и других точек в этом треугольнике нет. Тогда в оставшихся
шести треугольников разбиения лежат ещё 12 точек,
т.е. либо в некотором треугольнике лежат
по крайней мере 3 точки, не совпадающих с C (и тогда они искомые), либо
в каждом из оставшихся треугольников лежат ровно 2 точки.
Тогда выберем 2 точки в треугольнике соседнем к заштрихованному и добавим
точку C. Эти три точки, очевидно, искомые.
Задача 4:
Назовём трёхзначное число особенным, если из него можно вычеркнуть
цифру так, что образовавшееся число будет меньше суммы цифр
исходного трёхзначного. Сколько существует особенных чисел?Решение: Сумма цифр трёхзначного числа не превосходит 27, поэтому во всяком особенном числе есть цифра, не превосходящая 2. Тогда сумма цифр всякого особенного числа не больше 9 + 9 + 2 = 20, причём 20 достигается только в случае 229, 292 и 922. Так как ни одно из этих чисел не является особенным, сумма цифр особенного числа всегда меньше 20, значит, в особенном числе в разряде сотен или десятков присутствуют либо 0, либо 1. Допустим, что ни в разряде сотен, ни в разряде десятков ноль не стоит. Тогда особенное число имеет вид:
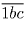 (или
(или 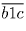 ). Так как число особенное,
выполняется неравенство:
). Так как число особенное,
выполняется неравенство: 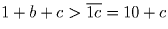 , откуда b > 9
— противоречие. Так как ноль в разряде сотен стоять не может (в
этом случае число не трёхзначное), приходим к выводу, что все
особенные числа имеют вид
, откуда b > 9
— противоречие. Так как ноль в разряде сотен стоять не может (в
этом случае число не трёхзначное), приходим к выводу, что все
особенные числа имеют вид 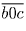 . С другой стороны, любое
число указанного вида — особенное (вычёркиваем ноль). В разряде
сотен может стоять любая цифра, отличная от нуля; в разряде единиц —
любая цифра. Всего имеется 9 • 10 возможностей, поэтому общее количество
особенных чисел 90.
. С другой стороны, любое
число указанного вида — особенное (вычёркиваем ноль). В разряде
сотен может стоять любая цифра, отличная от нуля; в разряде единиц —
любая цифра. Всего имеется 9 • 10 возможностей, поэтому общее количество
особенных чисел 90.Ответ: 90 чисел.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXIX олимпиада, 1998-1999 >> Заочный тур >> 9 класс | Убрать решения |