Задача 1:
10 векторов таковы, что длина суммы любых девяти из них
меньше длины всех 10. Доказать, что найдется ось, на которую каждый
из 10 векторов дает положительную проекцию.
Задача 2:
Функция f(x) определена и непрерывна на всей числовой оси.
Известно, что при любом фиксированном положительном x f(x + n)
стремится к нулю, при натуральном n, стремящемся к бесконечности.
Следует ли отсюда, что f(x) стремится к нулю, при x стремящемся к
бесконечности?
Задача 3:
Решить уравнение:
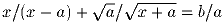
Задача 4:
Даны n вещественных чисел: x
1 ,x
2 ,…, x
n.
Доказать, что модуль хотя бы одного из чисел
x
1 + x
2 + … + x
k – x
k + 1 – … – x
n(при k = 1,2,3,...n, считать xn + 1 = 0)
не превосходит наибольшего из модулей xk.
Задача 5:
Вычислить без таблиц
tg ( π /11) • tg (2 π /11) • tg (3 π /11) • tg (4 π /11) • tg (5 π /11)