 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Заключительный этап всероссийской олимпиады >> XXV >> 11 класс | Убрать решения |
|
|
| XXV всероссийская математическая олимпиада школьников. Заключительный этап. 11 класс |
|
|
Существуют ли 19 попарно различных натуральных чисел с одинаковой суммой цифр таких, что их сумма равна 1999?
Решение:Ответ. Нет. Пусть сумма цифр каждого из чисел равна S = 9k + n, n = 0,1, … ,8. Тогда все эти числа имеют остаток n при делении на 9, и имеет место сравнение 19n = 18n + n ≡ 1999 (mod %)%9), откуда n ≡ 1 (mod %)%9, т.е. n = 1.
1) Пусть k = 0, т.е. S = 1. Рассмотрим 5 наименьших натуральных чисел с суммой цифр, равной 1. Это числа 1, 10, 100, 1000 и 10000. Но даже их сумма больше 1999.
2) Пусть k = 1, т.е. S = 10. Рассмотрим 19 наименьших натуральных чисел чисел с суммой цифр, равной 10. Это числа 19, 28, 37, 46, 55, 64, 73, 82, 91, 109, 118, 127, 136, 145, 154, 163, 172, 181, 190. Их сумма равна 1990 < 1999. Следующее натуральное число с суммой цифр, равной 10, есть 208, что по крайней мере на 18 больше любого из первых 19 чисел, и значит, сумма будет не менее 1990 + 18 = 2008 > 1999.
3) Пусть k ≥ 2, т.е. S ≥ 19. Но наименьшее число с суммой цифр не меньше 19 есть 199, а сумма любых 19 таких чисел будет заведомо больше 1999.
Таким образом, мы получили, что 19 чисел, удовлетворяющих условию, не существует.
Задача 2:Во всех рациональных точках вещественной прямой расставлены целые числа. Докажите, что найдётся такой отрезок, что сумма чисел на его концах не превосходит удвоенного числа в его середине.
Решение:Предположим противное, т.е. пусть существует такая расстановка целых чисел, что для любого отрезка AB с серединой C выполняется неравенство c < (a + b)/2, где a, b, c – соответственно числа, стоящие в точках A, B и C.
Пусть A, B, C, An, Bn, n = 1,2, … –
соответственно точки – 1, 1, 0,
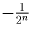 , ½n числовой прямой,
a, b, c, an, bn – целые числа,
записанные в этих точках.
, ½n числовой прямой,
a, b, c, an, bn – целые числа,
записанные в этих точках.
Тогда, по предположению, 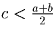 ,
, 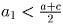 ,
,
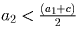 и т.д.
и т.д.
Отсюда следует, что max (a,c) > max(a1,a2), так как
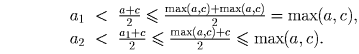
Аналогично, max (a1,a2) > max (a3,a4) > max (a5,a6) > … и max (b,c) > max (b1,b2) > max (b3,b4) > … . Таким образом, a2m < max (a,c) – m, b2m < max (b,c) – m и, значит, при некотором m будет выполнено неравенство a2m + b2m ≤ 2c. Противоречие, так как число c записано в середине отрезка A2mB2m .
Задача 3:Окружность, вписанная в четырёхугольник ABCD, касается его сторон DA, AB, BC, CD в точках K, L, M, N соответственно. Пусть S1, S2, S3, S4 – соответственно окружности, вписанные в треугольники AKL, BLM, CMN, DNK. К окружностям S1 и S2, S2 и S3, S3 и S4, S4 и S1 проведены общие внешние касательные, отличные от сторон четырёхугольника ABCD. Докажите, что четырёхугольник, образованный этими четырьмя касательными – ромб.
Решение:Обозначим искомый четырёхугольник RQFE (начиная с вершины ближайшей к окружности S1 по часовой стрелке. Как было показано в решении задачи 9.3, RQ\|KM\|EF, RE\|LN\|QF. Значит, образовавшийся четырёхугольник – параллелограмм. Используя то, что касательные к окружности, проведённые из одной точки, равны и AB + CD = AD + BC, получаем RQ + EF = RE + QF, так как (RQ + EF) – (RE + QF) = (a12 + a34) – (a41 + a23), где aij – длина общей внешней касательной к окружностям Si и Sj .
Значит, RQFE – ромб.
Задача 4:Задача 5:
Четыре натуральных числа таковы, что квадрат суммы любых двух из них делится на произведение двух оставшихся. Докажите, что по крайней мере три из этих чисел равны между собой.
Решение:Набор натуральных чисел, удовлетворяющий условию задачи, условимся называть хорошим.
Пусть существует хороший набор.
Ясно, что если (a,b,c,d) – хороший набор,
то и (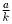 ,
, 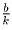 ,
, 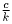 ,
, 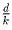 ) –
тоже хороший набор,
где k = НОД (a,b,c,d). Поэтому в дальнейшем считаем, что
НОД (a,b,c,d) = 1
) –
тоже хороший набор,
где k = НОД (a,b,c,d). Поэтому в дальнейшем считаем, что
НОД (a,b,c,d) = 1
Пусть одно из данных чисел, например a, имеет нечётный простой делитель p. Тогда суммы b + c, c + d, b + d и, следовательно, сами числа b, c и d делятся на p (ибо, например, 2d = (b + d) + (c + d) – (b + c)), что противоречит нашему предположению Значит, числа a, b, c, d – степени двойки. Упорядочив данные числа в порядке возрастания, получим a = 2m, b = 2n, c = 2r, d = 2s, где 0 = m ≤ n ≤ r ≤ s, r ≥ 1 (иначе m = n = r = 0, значит, a = b = c).
Тогда число (a + c)² = (1 + 2r)² – нечётно и не может делиться на чётное число bd.
Задача 6:Докажите, что три выпуклых многоугольника на плоскости нельзя пересечь одной прямой тогда и только тогда, когда каждый многоугольник можно отделить от двух других прямой (т. е. существует прямая такая, что этот многоугольник и два остальных лежат по её разные стороны).
Решение:Пусть каждый из многоугольников A, B, C можно отделить от двух других. Докажем, что их нельзя пересечь одной прямой. Предположим противное: X, Y, Z – соответственно точки многоугольников A, B, C, лежащие на одной прямой. Тогда одна из точек, например Y, лежит на прямой между X и Z. Следовательно, B нельзя отделить от A и C, так как в противном случае точку Y, лежащую между двумя другими X и Z, нужно отделить от этих точек одной прямой, что невозможно.
В обратную сторону утверждение можно доказать двумя способами.
1) Рассмотрим треугольники с вершинами X ∈ A, Y ∈ B, Z ∈ C. Пусть из всех таких треугольников наименьшую высоту имеет треугольник X0Y0Z0 и эта высота проведена из вершины Y0. Тогда прямая, перпендикулярная высоте и проходящая через середину высоты, не пересекает многоугольники B, A и C, так как, в противном случае, существовал бы треугольник с меньшей высотой, выходящей из Y0.
2) Рассмотрим две внешние касательные к многоугольникам A и C. Тогда они не могут пересекать B. Если мы сдвинем немного ту, которая лежит ближе к B, в направлении к многоугольнику B, то получим прямую, отделяющую B от A и C.
Задача 7:
Через вершину A тетраэдра ABCD проведена плоскость, касательная к описанной около него сфере. Докажите, что линии пересечения этой плоскости с плоскостями граней ABC, ACD и ABD образуют шесть равных углов тогда и только тогда, когда AB • CD = AC • BD = AD • BC.
Решение:Проведём плоскость, параллельную касательной плоскости,
пересекающую рёбра AB, AC и AD в точках B1, C1 и D1
соответственно. Рассмотрим плоскость ABC. Нетрудно видеть, что
∆ AB1C1 подобен треугольнику ACB. Откуда
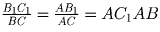 .
Аналогично,
.
Аналогично,
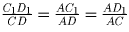 и
и
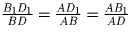 .
.
Из этих равенств вытекает, что
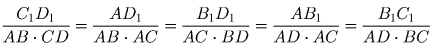
Значит, треугольник A1B1C1 равносторонний тогда и только тогда, когда AB • CD = AC • BD = AD • BC.
Осталось заметить, что углы, образуемые указанными в условии линиями пересечения, соответственно равны углам треугольника A1B1C1.
Задача 8:В микросхеме 2000 контактов, первоначально любые два контакта соединены отдельным проводом. Хулиганы Вася и Петя по очереди перерезают провода, причем Вася (он начинает) за ход режет один провод, а Петя – либо два, либо три провода. Хулиган, отрезающий последний провод от какого-либо контакта, проигрывает. Кто из них выигрывает при правильной игре?
Решение:Докажем, что выигрывает Петя. Разобьем контакты на четыре одинаковых группы A, B, C и D. В каждой группе пронумеруем контакты числами от 1 до 500. Мысленно покрасим в черный цвет провода между контактами с разными номерами, и в белый цвет – между контактами с одинаковыми номерами.
Петя будет отвечать на любой ход Васи так, чтобы для каждого номера k от контактов Ak, Bk, Ck и Dk отходило поровну черных проводов, и если у одного из контактов больше нет белых проводов, то их не было бы и у других контактов с таким же номером. До начала игры это условие, очевидно, выполняется. Именно благодаря этому условию у Пети всегда будет возможность ответить на ход Васи.
Теперь подробнее опишем Петину стратегию. Сначала рассмотрим случай, когда Вася режет черный провод. Если Вася перерезает провод между контактами одной группы, например, провод AiAj, то Петя перережет провода BjBj, CiCj и DjDj. Если Вася перерезает провод между проводами из разных групп и с разными номерами, например, провод AiBj, то Петя в ответ перережет провода AjBi, CiDj и CjDi. Такие ходы Петя может сделать, так как из возможности отрезать один провод от некоторого контакта следует возможность отрезать по одному проводу от вершин с таким же номером.
Остается рассмотреть случай, когда Вася перерезал белый провод, то есть, провод между контактами из разных групп, но с одинаковыми номерами. Рассмотрим четыре контакта Ak, Bk, Ck и Dk. Первоначально любые два из них соединены проводом. После того, как Вася перерезал первый из этих проводов, например, провод AkBk, Петя перережет два провода так, чтобы между этих контактов осталось три провода, имеющие один общий конец (например, Петя может перерезать провода BkCk и CkAk, после чего останутся провода AkDk, BkDk и CkDk, что подтверждает возможность такого хода). Если же Вася когда-нибудь перережет один из этих трех проводов, то от одного из контактов Ak, Bk или Ck он отрежет последний провод к контактам с этим же номером k, следовательно, от этого контакта будет отходить провод к контакту с другим номером. Значит, и от трех других контактов с номером k будут отходить провода к контактам с другим номером, следовательно, Петя может перерезать два оставшихся провода между контактами с номером k, что он и сделает.
Отметим, что каждый раз после хода Пети описанное выше условие выполняется. Следовательно, Петя всегда сможет сделать ход, и, так как количество проводов конечно, проиграет Вася.
| Задачная база >> Соревнования всероссийского уровня >> Заключительный этап всероссийской олимпиады >> XXV >> 11 класс | Убрать решения |