 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Кубок памяти Колмогорова >> IV кубок >> Турнир матбоёв >> 1-й тур >> Высшая лига | Убрать решения |
|
|
| Соревнования всероссийского уровня. Кубок памяти Колмогорова. IV кубок. Турнир матбоёв. 1-й тур. Высшая лига |
|
|
При некотором натуральном k > 1 нашлись взаимно-простые числа a и b, a > b, что ak – bk есть степень a – b. Чему могло равняться a – b?
(С.А.Злобин)
Задача 2:Для положительных чисел x, y, z выполняется равенство Докажите, что
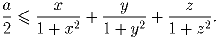
(С.А.Злобин)
Задача 3:В компании у каждых двух людей ровно пять общих знакомых. Докажите, что количество знакомств (пар знакомых) кратно трем.
(Ю.М.Лившиц)
Задача 4:Докажите, что поверхность кубика нельзя оклеить в один слой без пропусков 23 одинаковыми прямоугольниками. Перегибать прямоугольники разрешается по линиям, параллельным сторонам.
(С.Г.Волченков)
Задача 5:Различные простые числа p и q таковы, что при некотором целом k > 2 число p² + kpq + q² – точный квадрат. Докажите, что (p – 2)(q – 2) ≤ k + 2.
(И.И.Богданов, С.Л.Берлов)
Задача 6:У каждого из двух равных правильных додекаэдров отметили по 9 вершин. Докажите, что первый додекаэдр можно так совместить со вторым, чтобы по крайней пять его отмеченных вершин совпали с отмеченными вершинами второго.
(С.Г.Волченков)
Задача 7:A1, B1 и C1 – проекции точки P, лежащей внутри остроугольного треугольника ABC, на стороны BC, CA и AB соответственно. Прямая A1C1 пересекает прямую AC в точке K. Описанная окружность треугольника A1B1C1 вторично пересекает сторону AC в точке L. Докажите, что KP ⊥ BL.
(Д.Джукич)
Задача 8:На съезде учителей делегаты сидели в 50 рядов по 100 человек (расположенных в виде прямоугольника). Ни у одного из делегатов нет в карманах долларов и рублей одновременно. Каждый делегат выяснил, что у всех его соседей справа, слева, спереди и сзади в сумме столько же рублей, сколько и долларов. Докажите, что у каждого делегата в карманах нет ни долларов, ни рублей.
(Р.Садыков, Д.Шаповалов)
Задача 9:Через центр окружности ω с центром O проведены 7 прямых. В каждый из 14 углов, на которые они разбивают плоскость, вписано по окружности так, что каждая окружность касается сторон своего угла в точках, лежащих на окружности ω . Обозначим эти точки A1, …, A14 (в том порядке, в котором они идут на окружности по часовой стрелке). На лучах OAi (i = 1,2, … ,14) выбраны точки Bi, лежащие вне окружности ω , таким образом, что отрезки B1B2, B2B3, …, B13B14 касаются окружностей, вписанных в соответствующие углы. Докажите, что отрезок B14B1 тоже касается окружности, вписанной в свой угол.
(Д.Джукич)
Задача 10:Какое максимальное число действительных решений может иметь уравнение
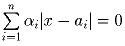 ,
если известно, что множество его решений в действительных числах конечно?
,
если известно, что множество его решений в действительных числах конечно?
(А.Я.Белов)
| Задачная база >> Соревнования всероссийского уровня >> Кубок памяти Колмогорова >> IV кубок >> Турнир матбоёв >> 1-й тур >> Высшая лига | Убрать решения |