 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Кубок памяти Колмогорова >> IV кубок >> Турнир матбоёв >> 2-й тур >> Высшая лига | Убрать решения |
|
|
| Соревнования всероссийского уровня. Кубок памяти Колмогорова. IV кубок. Турнир матбоёв. 2-й тур. Высшая лига |
|
|
Сколько существует операций *, заданных на множестве 1, 2, , 101 и обладающих следующими свойствами:
Касательная в точке A к описанной окружности треугольника ABC пересекает продолжение средней линии треугольника, параллельной стороне BC, в точке A′. Точки B′ и C′ определяются аналогично. Докажите, что точки A′, B′, C′ лежат на одной прямой, перпендикулярной прямой Эйлера треугольника.
Задача 3:
В связном графе 2n вершин, степень каждой вершины равна трем. Докажите, что количество способов раскрасить ребра этого графа в три цвета так, чтобы в каждой вершине сходились ребра разных цветов, не превосходит 3 • 2n.
Задача 4:
Для каких натуральных N найдутся такие натуральные x, y, z, что (x + y + z)² = Nxyz?
Задача 5:
Двое играют в крестики-нолики на бесконечной клетчатой полосе ширины 1. Первый ходит одним крестиком, второй – сотней ноликов (не обязательно подряд). Цель первого – получить три крестика, один из которых стоит точно посередине между двумя другими, цель второго – помешать первому это сделать. Какого минимального числа ходов достаточно первому для того, чтобы обеспечить себе победу независимо от ходов второго?
Задача 6:
Найдите все непрерывные функции 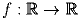 ,
которые при всех действительных x
удовлетворяют уравнению f(f(x)) = f(x) + 2x.
,
которые при всех действительных x
удовлетворяют уравнению f(f(x)) = f(x) + 2x.
Задача 7:
Пусть Q(x) – многочлен ненулевой степени с целыми коэффициентами, который не раскладывается в произведение многочленов ненулевой степени с рациональными коэффициентами. Докажите, что найдутся такие натуральное число n и простое число p, что число Q(n) делится на p, но не делится на p².
Задача 8:
Дан пятиугольник ABCDE в котором AB = BC и ∠ A = ∠ C = 90. Точка Fна
стороне ED такова, что 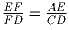 . Докажите,
что ∠ ACF = ∠ ABE.
. Докажите,
что ∠ ACF = ∠ ABE.
Задача 9:
Из каждой вершины (не обязательно выпуклого) многоугольника можно провести диагональ длины, не превосходящей 1, целиком лежащую внутри многоугольника. Докажите, что у этого многоугольника найдется сторона, длина которой не превосходит 1.
Задача 10:
Пусть n ≥ 2 – натуральное число. Докажите, что
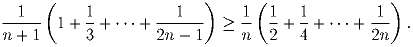
| Задачная база >> Соревнования всероссийского уровня >> Кубок памяти Колмогорова >> IV кубок >> Турнир матбоёв >> 2-й тур >> Высшая лига | Убрать решения |