 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Кубок памяти Колмогорова >> IV кубок >> Турнир матбоёв >> 3-й тур >> Первая лига | Убрать решения |
|
|
| Соревнования всероссийского уровня. Кубок памяти Колмогорова. IV кубок. Турнир матбоёв. 3-й тур. Первая лига |
|
|
На окружности отмечены 2n точек так, что никакие три хорды с концами в этих точках не пересекаются в одной точке, лежащей внутри окружности. Разобьем отмеченные точки на n пар, и в каждой паре соединим точки отрезком. Число точек пересечения проведенных n отрезков назовем характеристикой разбиения. Найдите среднее арифметическое характеристик по всем разбиениям.
(Сообщил И. Богданов)
Задача 2:В лагерь приехали m мальчиков и d девочек. Каждая девочка знакома не более, чем с 10 мальчиками, а каждый мальчик – не менее, чем с одной девочкой. Оказалось, что у каждого мальчика больше знакомых девочек, чем у любой знакомой с ним девочки – знакомых мальчиков. Докажите, что d ≥ 1,1m.
(Д.В. Карпов)
Задача 3:Точки бесконечной полоски ширины 1 раскрашены в два цвета. Докажите, что для любого положительного числа r найдутся две точки одного цвета на расстоянии r.
(А.Я. Канель-Белов)
Задача 4:Окружности S1 и S2 пересекаются в точках A и B. Через точку B проведена прямая l, вторично пересекающая окружности S1 и S2 в точках C и D соответственно. Точка K на окружности S2 такова, что прямые CA и AK перпендикулярны. Точка L на окружности S1 такова, что прямые DA и AL перпендикулярны. Точка P симметрична точке A относительно прямой l. Докажите, что точки A, K, L и P лежат на одной окружности.
(Д. Джукич)
Задача 5:В арифметической прогрессии, состоящей из натуральных чисел, есть член, десятичная запись которого содержит ровно две единицы (и, возможно, какие-то другие цифры). Докажите, что в ней есть член, десятичная запись которого содержит ровно 2000 единиц (и, возможно, какие-то другие цифры).
(А.С. Голованов)
Задача 6:Докажите, что неравенство 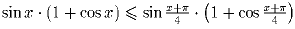 справедливо для любого
справедливо для любого 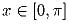 .
.
(T.Kubo)
Задача 7:Даны натуральное число k и многочлены R(x) и S(x) с целыми коэффициентами. Известно, что при любом целом x число R(S(x)) – x делится на k. Докажите, что число S(R(x)) – x тоже делится на k при любом целом x.
(И.И.Богданов)
Задача 8:Из точки P в пространстве проведены лучи k, l и m. На луче k взята точка A. Докажите, что найдется единственная пара точек B ∈ l и C ∈ m, для которых выполнены равенства PA + AB = PC + CB и PB + BC = PA + AC.
Задача 9:Известно, что 3a + 2b + 3c = 0. Докажите, что уравнение ax³ + bx + c = 0 имеет хотя бы один корень на интервале (0,3).
(К.А.Кноп)
Задача 10:Различные натуральные числа a и b таковы, что (a – b)4 = a³ – b³. Докажите, что число 9a – 1 есть куб натурального числа.
(Д. Джукич)
| Задачная база >> Соревнования всероссийского уровня >> Кубок памяти Колмогорова >> IV кубок >> Турнир матбоёв >> 3-й тур >> Первая лига | Убрать решения |