 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Кубок памяти Колмогорова >> IV кубок >> Турнир матбоёв >> 4-й тур >> Высшая лига. Бои за 1-4 места. | Убрать решения |
|
|
| Соревнования всероссийского уровня. Кубок памяти Колмогорова. IV кубок. Турнир матбоёв. 4-й тур. Высшая лига. Бои за 1-4 места. |
|
|
Назовем разбиение клетчатой доски 200 × 200 на доминошки (то есть прямоугольники из двух клеток) удачным, если любое разбиение этой доски на доминошки имеет с данным четное число общих доминошек. Сколько существует удачных разбиений?
Задача 2:
В вершинах правильного 101-угольника расставлены единицы. За один ход разрешается выбрать четыре подряд стоящие числа, вычесть по 1 из двух средних и прибавить по 1 к двум крайним. Можно ли не более чем за 10000 таких ходов получить расстановку, в которой все числа, кроме одного, равны нулю?
Задача 3:
Для положительных a1, a2, …, an
докажите неравенство 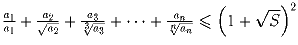 , где S = a1 + a2 + … + an.
, где S = a1 + a2 + … + an.
Задача 4:
В графе существует остовное дерево ровно с n висячими вершинами и остовное дерево ровно с m висячими вершинами, n ≤ k ≤ m. Докажите, что в этом графе существует остовное дерево ровно с k висячими вершинами.
Задача 5:
На окружности S выбраны точки A и B. Точка C – середина одной из дуг AB, а D – некоторая точка отрезка AB. Окружность S1 касается отрезков BD (в точке B1), CD и окружности S. Окружность S2 касается продолжения отрезка AB за точку B (в точке B2), окружности S (в точке K) и продолжения отрезка CD за точку D. Доказать, что ∠ B1KB2 – прямой.
Задача 6:
Сколько существует натуральных решений уравнения
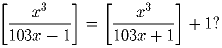
Задача 7:
Выпуклый многогранник M с n вершинами находится внутри куба с ребром 1.
Все грани M – треугольники. Докажите, что существует тетраэдр объема не
больше 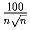 с вершинами в вершинах многогранника
M.
с вершинами в вершинах многогранника
M.
Задача 8:
В последовательности натуральных чисел (xn),
n ≥ 1,
выполняется соотношение 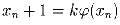 ,
где
,
где 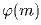 обозначает количество натуральных чисел, не
превосходящих m и взаимно простых с m. Найдите все такие натуральные k > 1,
что при любом натуральном x1 > 1 последовательность (xn)
ограничена.
обозначает количество натуральных чисел, не
превосходящих m и взаимно простых с m. Найдите все такие натуральные k > 1,
что при любом натуральном x1 > 1 последовательность (xn)
ограничена.
Задача 9:
Окружность проходит через вершины A и C остроугольного треугольника ABC и пересекает стороны AB и BC в точках D и E. Точки D1 и E1 симметричны точкам D и E соответственно относительно основания высоты треугольника, опущенной на сторону AC. Прямые CD1 и AE1 пересекаются в точке K. Докажите, что ∠ AKC = ∠ ABC.
Задача 10:
Найдите все функции 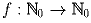 такие, что f(x² + y²) = xf(x) + yf(y). (Здесь
такие, что f(x² + y²) = xf(x) + yf(y). (Здесь
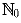 – множество целых неотрицательных чисел.)
– множество целых неотрицательных чисел.)
| Задачная база >> Соревнования всероссийского уровня >> Кубок памяти Колмогорова >> IV кубок >> Турнир матбоёв >> 4-й тур >> Высшая лига. Бои за 1-4 места. | Убрать решения |