 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Турниры журнала ``Квант'' >> Математика 6-8, 2001 >> Личная олимпиада | Убрать решения |
|
|
| Заключительный конкурс "Математика 6-8" журнала "Квант". Личная олимпиада |
|
|
(С. Г. Волченков)
Задача 2: В каждой клетке доски размером 16 × 30 сидит по жуку. Могут ли жуки перелететь на доску размером 15 × 32, в каждую клетку по одному жуку, чтобы жуки, бывшие соседями на доске 16 × 30, оказались соседями и на новой доске? (Соседи – жуки, сидящие в клетках с общей стороной.)(И. Жук, г. Гродно)
Задача 3: В следующих многозначных числах цифры заменены буквами (одинаковые цифры – одинаковыми буквами, а разные – разными). Оказалось, что ДЕВЯНОСТО делится на 90, а ДЕВЯТКА делится на 9. Может ли СОТКА делиться на 9? Задача 4: Можно ли первые 2001 натуральных чисел расставить по кругу так, чтобы каждое число делилось на разность своих соседей?Задача 5: Натуральное число разрешено увеличить на любое целое число процентов от 1 до 100 процентов, если при этом получаем натуральное число. Найдите наименьшее натуральное число, которое нельзя при помощи таких операций получить из числа 1.
(А. Шаповалов)
Задача 6: Оси Ox и Oy и прямые y = ax + b, y = bx + c, y = cx + a расположены так, как показано на рисунке. Укажите ось Ox и положительное направление на ней.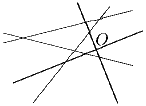
(С.Токарев)
Задача 7: Двое играют в шахматы, а еще шестеро желающих сыграть образуют очередь. Проигравший партию становится в конец очереди; тот, чья очередь подошла, играет с победителем и так далее. Может ли в какой-то момент оказаться так, что каждые двое сыграли между собой ровно один раз?
(С. Токарев)
| Задачная база >> Соревнования всероссийского уровня >> Турниры журнала ``Квант'' >> Математика 6-8, 2001 >> Личная олимпиада | Убрать решения |