Задача 1:
Врач дал больному пакетик с таблетками и велел принимать ежедневно
по четверти таблетки. Тот так и сделал, причем каждый раз он вынимал
из пакетика наугад что попадется. Если попадалась целая таблетка, он
разламывал ее на 4 части, одну из которых съедал, а остальные
возвращал обратно; если же попадалась ранее отломленная четвертинка,
он ее просто проглатывал. После месяца такого лечения в пакетике
осталось в 8 раз больше четвертинок, чем целых таблеток, а еще через
три месяца осталось лишь 5 целых таблеток. Сколько осталось
четвертинок?
Задача 2:
Найдите все тройки натуральных чисел (a,b,c) такие, что числа
a³ + 6ab + 20, b³ + 6bc + 20, c³ + 6ca + 20 являются точными кубами.
Задача 3:
N различных натуральных чисел, не превосходящих 1000, выписаны
по кругу так, что сумма любых двух из них, стоящих через одно,
делится на 3. Найдите наибольшее возможное значение N.
Задача 4:
На шахматной доске стояло 16 королей, каждый из которых находился
под боем хотя бы одного из остальных. После того, как несколько
королей убрали, никакие два из оставшихся друг друга не стали бить.
Какое наибольшее число королей могло остаться?
Задача 5:
На плоской поверхности лежат несколько круглых монет. Докажите,
что для любой точки P этой поверхности, не покрытой монетами,
найдется монета, вид на которую из P не загорожен другими монетами.
Задача 6:
Последовательность a
n задана условиями a
1 = 1,
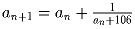
при всех n ≥ 1. Доказать, что
a
1000 < 10.
Задача 7:
Несколько точек разбивают окружность на дуги. По окружности
прыгает блоха. Перед каждым своим прыжком она вычисляет длину дуги,
на которой находится, а затем прыгает так, чтобы сместиться по
часовой стрелке на дугу вычисленной длины. Докажите, что блоха
побывает на всех дугах.
Задача 8:
На стороне AC треугольника ABC находится точка B
1. На
сторонах AB и BC постройте соответственно точки C
1 и A
1
так, чтобы площади треугольников AB
1C
1, A
1BC
1 ,A
1B
1C были
равны.


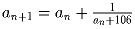 при всех n ≥ 1. Доказать, что
a1000 < 10.
Задача 7:
Несколько точек разбивают окружность на дуги. По окружности
прыгает блоха. Перед каждым своим прыжком она вычисляет длину дуги,
на которой находится, а затем прыгает так, чтобы сместиться по
часовой стрелке на дугу вычисленной длины. Докажите, что блоха
побывает на всех дугах.
Задача 8:
На стороне AC треугольника ABC находится точка B1. На
сторонах AB и BC постройте соответственно точки C1 и A1
так, чтобы площади треугольников AB1C1, A1BC1 ,A1B1C были
равны.
при всех n ≥ 1. Доказать, что
a1000 < 10.
Задача 7:
Несколько точек разбивают окружность на дуги. По окружности
прыгает блоха. Перед каждым своим прыжком она вычисляет длину дуги,
на которой находится, а затем прыгает так, чтобы сместиться по
часовой стрелке на дугу вычисленной длины. Докажите, что блоха
побывает на всех дугах.
Задача 8:
На стороне AC треугольника ABC находится точка B1. На
сторонах AB и BC постройте соответственно точки C1 и A1
так, чтобы площади треугольников AB1C1, A1BC1 ,A1B1C были
равны.