 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Уральский турнир юных математиков >> IV турнир (осень, 1994) >> Математический аукцион | Убрать решения |
|
|
| IV Уральский турнир юных математиков. Челябинск. Осень, 1994. Математический аукцион |
|
|
Решение: 139 × 408, 247 × 158, 438 × 217, 463 × 207 483 × 109, 745 × 126
Задача 2: Найдите трехзначные натуральные числа, которые при сложении со своим обращенным числом дают числа, делящиеся на число
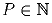 .
.Задача 3: Найдите натуральные трехзначные числа, квадраты которых оканчиваются на три одинаковых отличных от нуля цифры.
Решение: напр. 462
Задача 4: Какие четырехзначные числа, состоящие из цифр 1,2,3 делятся на 9?
Задача 5: Найти все натуральные числа x,y,z, для которых число 1/x + 1/y + 1/z является целым числом.
Решение:
(1,1,1); (3,3,3); (2,4,4); (2,3,6); (1,2,2)
Задача 6: При каких натуральных n число 2n + 65 является квадратом целого числа? Решение: (4,10)
Задача 7: Найти целые числа p, при которых уравнение x² + px + 1994 = 0 имеет целые корни.
Задача 8: Найдите все целые решения уравнения 5z² – 8y² + x² – 10yz = 1, удовлетворяющие условию: 0 ≤ x + y + z ≤ 100.
Задача 9: Решите уравнение
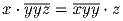 .
.Решение: 1664, 1995, 2665, 4998
| Задачная база >> Соревнования всероссийского уровня >> Уральский турнир юных математиков >> IV турнир (осень, 1994) >> Математический аукцион | Убрать решения |