 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Уральский турнир юных математиков >> XV турнир (февраль, 2000) >> Турнир матбоёв >> Математический бой N2 >> Младшая группа, первая лига | Убрать решения |
|
|
| XV Уральский (VIII кировский) турнир юных математиков. Турнир матбоёв. Математический бой N2. Младшая группа, первая лига |
|
|
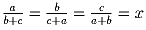 ?
?
(Украинская олимпиада, 1987)
Задача 3: Десять гирь весом 1, 2, …, 10 г разделили на две группы так, что в каждой группе больше одной гири. Докажите, что можно положить на одну чашу весов какие-то гири (одну или несколько) из одной группы, а на другую – какие-то гири из другой группы так, что весы окажутся в равновесии.
(И.Рубанов, К.Кноп)
Задача 4: В трапеции ABCD диагональ BD перпендикулярна боковой стороне AB и AB = BC = BD. Докажите, что CD = CO (O – точка пересечения диагоналей).
(Л.Медников)
Задача 5: Одно и то же натуральное число поделили с остатком на 3, на 18 и на 48. Сумма остатков оказалось равна 39. Найдите остаток от деления этого числа на 3.
(К.Кохась)
Задача 6: В клетках таблицы 100 × 100 расставлены попарно различные числа. Каждую минуту каждое из чисел меняется на наибольшее из чисел, стоящих в соседних с ним по стороне клетках. Могут ли через 4 часа все числа в таблице оказаться одинаковыми?
(Украинская олимпиада, 593, вариант)
Задача 7: Все ученики математического кружка, кроме троих, учатся в 5 классе, все, кроме троих, учатся в шестом классе, и все, кроме двоих, семиклассники. Сколько всего человек занимается в этом кружке?
(126, Жюри)
Задача 8: Написанное на доске число можно умножить или разделить на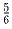 или
или 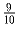 . Можно ли из 1 получить другое целое число?
. Можно ли из 1 получить другое целое число?
(А.Проскурников$+$жюри)
| Задачная база >> Соревнования всероссийского уровня >> Уральский турнир юных математиков >> XV турнир (февраль, 2000) >> Турнир матбоёв >> Математический бой N2 >> Младшая группа, первая лига | Убрать решения |