Задача 1: В алфавите языка племени МУМБО-ЮМБО всего две буквы А и Б. Два слова означают одно и то же, если одно получается из другого при помощи некоторого числа таких операций: вычёркивания трёх подряд идущих букв А, вставки трех букв А в любое место, замены любого набора стоящих рядом букв АБА на набор стоящих рядом букв БААБ или обратной замены. Верно ли, что слово АББ…Б и слово ББ…БА (в каждом из этих слов буква Б встречается 2000 раз) означают одно и то же?

(А.Штерн)

Задача 2: Найдите все пятизначные числа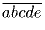 , которые делятся на .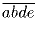

(Украинская олимпиада, 1982)

Задача 3: В чемпионате по рыбной ловле участвовало несколько рыбаков. Известно, что победитель (поймавший наибольшее число рыб) поймал ровно в 4 раз меньше рыб, чем все остальные участники вместе взятые. Рыбак, занявший третье место, поймал ровно в 9 раз меньше, чем все остальные, а рыбак, оказавшийся на последнем месте, поймал ровно в 10 раз меньше, чем все остальные. Сколько рыбаков участвовало в соревновании?

(С.Берлов и С.Иванов)

Задача 4: Пусть M и N – середины сторон AB и CD четырехугольника ABCD. Известно, что серединные перпендикуляры к MN, AC и BD пересекаются в одной точке. Докажите, что AB = CD.

(С.Берлов)

Задача 5: Остап Бендер дает сеанс одновременной игры 45 шахматистам, сидящим по кругу. Напротив некоторых из шахматистов стоят стулья. Остап садится на стул перед шахматистом, и, сделав ход, переходит к следующему по часовой стрелке шахматисту. При этом он передвигает стул, если перед следующим шахматистом стула нет. Все стулья одинаковы. Могло ли случиться так, что в течение 2000 ходов Остапа ни разу не повторилось расположение стульев и Остапа (считается, что за это время ни одна из партий не закончится)?

Задача 6: Сумма 10 натуральных чисел равна 99. Найдите максимальное возможное значение их (всех десяти!) наибольшего общего делителя.

(Киевская олимпиада, 1979)

Задача 7: Во дворе стоит 30 столбов, изначально между любыми двумя столбами натянут провод. Каждое утро по дороге в школу хулиган Вася срывает 29 проводов. Каждый вечер электрик Петров восстанавливает провода, отходящие от некоторого столба. Докажите, что Вася может действовать так, чтобы однажды утром после очередного акта вандализма осталось менее 30 проводов.

(А.Пастор)

Задача 8: В записи 1999-значного числа использовано 1000 девяток, 998 двоек и одна семерка. После вычеркивания одной цифры это число стало делится на 7 без остатка. Какую цифру вычеркнули?

(Р.Женодаров)