 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Уральский турнир юных математиков >> XVII турнир (февраль, 2001) >> Математическая карусель >> Исходные задачи.Младшая группа. | Убрать решения |
|
|
| XVII Уральский (IX кировский) турнир юных математиков. Математическая карусель. Исходные задачи.Младшая группа. |
|
|
Найти число, которое, будучи умножено на 3, а затем разделено на 5, увеличено на 6, после чего из него извлечён квадратный корень, отнята единица и результат возведён в квадрат, даст 4.
(Парамадисвара)
Решение:5
Задача 2:«Решить в натуральных числах систему: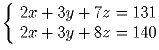 .» Сколько всего решений у этой системы?
.» Сколько всего решений у этой системы?
(Лебег)
Решение:12 решений
Задача 3:Какое число, будучи прибавлено к девяти, даст свой ушестерённый квадратный корень?
(Абен-Дреат)
Решение:9
Задача 4:Некто купил 30 птиц за 30 монет, из числа этих птиц за каждые 3 воробья заплачена 1 монета, за каждые 2 горлицы – также 1 монета, и, наконец, за каждого голубя – по 2 монеты. Сколько птиц каждой породы?
(Леонардо Фибоначчи)
Решение: 9 воробьёв, 10 горлиц и 11 голубей Задача 5:Некто имеет работников и деньги. Если он даст каждому работнику 5 монет, у него останется 30, а если 7, то не хватит 30. Спрашивается, сколько у него работников?
(рукопись Мюнхенского собрания)
Решение: 30 работников Задача 6:Разложить дробь 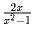 на сумму двух дробей вида
на сумму двух дробей вида
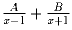 .
.
(Огюстен Луи Коши)
Решение: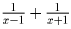
Некто согласился работать с условием получить в конце года одежду и 10 флоринов. Но по истечении 7 месяцев прекратил работу и при расчете получил одежду и 2 флорина. Во сколько ценилась одежда?
(Христоф Рудольф)
Решение: флорина
Задача 8:
флорина
Задача 8: Собака гонится за кроликом, находящимся в 150 футах от неё. Она делает прыжок в 9 футов каждый раз, когда кролик прыгает на 7 футов. Сколько прыжков должна сделать собака, чтобы догнать кролика?
(рукописный сборник ``Задачи для изощренного ума'')
Решение: 75 прыжков Задача 9:Найти сумму всех членов прогрессии: 3, 7, 11, 15, , 79
(Ал-Кархи)
Решение: 820 Задача 10:Найти число, четвертая степень которого, деленная на половину самого числа и увеличенная на 14¼, равнялась бы 100.
(Леонард Эйлер)
Решение: Задача 11:
Задача 11: Трое выиграли некоторую сумму денег. На долю первого пришлась 1/4 этой суммы, на долю второго – 1/7, а на долю третьего – 17 флоринов. Как велик весь выигрыш?
Решение: 28 флоринов Задача 12:Какое число следует прибавить к числителю и знаменателю дроби 3/11, чтобы получить дробь, равную 5/9 ?
(Желен)
Решение:7
Задача 13:Имеется 9 слитков золота и 11 слитков серебра. Их взвесили (золото – на левую чашу весов, серебро – на правую), и весы остались в равновесии. После того, как слиток золота переложили на правую чашу, а слиток серебра – на левую, левая чаша стала легче на 13 ланов. Каков вес одного слитка золота?
(Китай)
Решение:35,75 лана
Задача 14:Найти число, которое, будучи увеличено двумя третями самого себя и единицей, даёт 10.
(Бега Эддин)
Решение: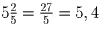
| Задачная база >> Соревнования всероссийского уровня >> Уральский турнир юных математиков >> XVII турнир (февраль, 2001) >> Математическая карусель >> Исходные задачи.Младшая группа. | Убрать решения |